Линейные уравнения и уравнения Бернулли

Рассмотрим уравнения вида

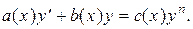(1)

Здесь функции 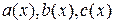непрерывны на промежутке .

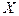Заметим, что при 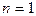получим уравнение с разделяющимися переменными.

Определение. При 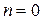уравнение (1) называется линейным. При 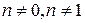оно называется уравнением Бернулли.

Уравнение (1) (и линейное и Бернулли) можно решить по следующему плану:

Решение ищется в виде произведения функций

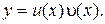(2)

Подставив эту функцию в (1), получим

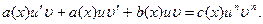
Сгруппируем слагаемые слева:

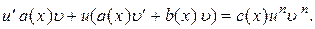(3)

Чтобы упростить это уравнение, подберем функцию 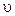так, чтобы

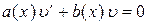. (4)

Это уравнение с разделяющимися переменными. Пусть

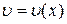(5)

есть какое-нибудь частное ненулевое решение уравнения (4). После подстановки этой функции в (3) получим более простое уравнение относительно неизвестной функции :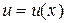

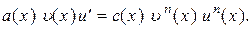(6)

Если уравнение (1) линейно, то есть 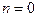, то уравнение (6) можно

разрешить относительно :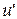

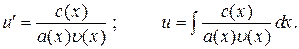
В случае уравнения Бернулли, то есть при 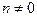, уравнение (6) является

уравнением с разделяющимися переменными.

Определив отсюда или из (6) функцию u, запишем решение в виде (2).

Таким образом, решение уравнения (1) сводится к решению двух уравнений с разделяющимися переменными (4), (6). Еще раз отметим, что мы ищем одно ненулевое частное решение уравнения (4) и общее решение уравнения (6).

Пример 1. Решить задачу Коши:

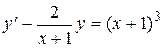(7)

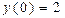(8)

Уравнение (7) является линейным. Ищем общее решение уравнения (7) в виде

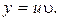(9)

Подставим это выражение в (7):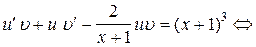

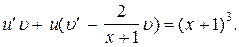(10)

Подберем функцию 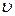так, чтобы

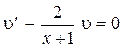(11)

Это уравнение с разделяющимися переменными. Найдем частное решение уравнения (11) тождественно не равное 0.

Разделив переменные, получим: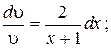

Проинтегрируем это равенство: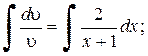

Отсюда: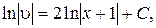

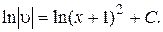
При 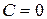одно из частных решений есть:

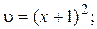(12)

Подставим это выражение в (10). Учитывая (11), получим

.

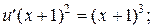
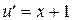Следовательно,

Отсюда и из (12) получим общее решение уравнения (7):

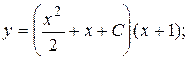(13)

Подставив сюда начальное условие (8), получим: .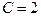

Ответ: .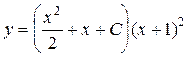

Пример 2 Решить уравнение

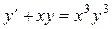(14)

Это уравнение Бернулли. Решаем его по тому же плану:

Ищем решение в виде: 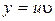. Тогда из (14) получим:

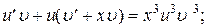(15)

Функцию 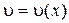найдем из уравнения: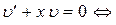

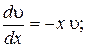
Найдем ненулевое частное решение. Для этого "разделим" переменные:

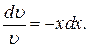
Проинтегрируем это равенство и найдем частное ненулевое решение:

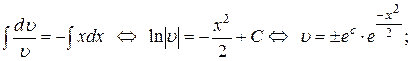
Подставим в (15) частное решение

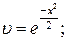(16)

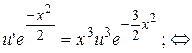
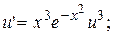(17)

Это уравнение с разделяющимися переменными относительно функции .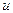

1). 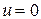- частное решение (17). При этом .

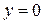2). В области, где 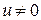разделим переменные и проинтегрируем:

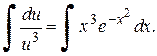
Следовательно:

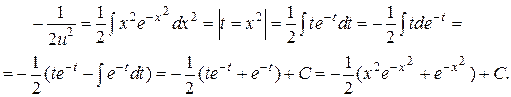
Отсюда выразим u: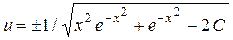

Учитывая (19) найдем: .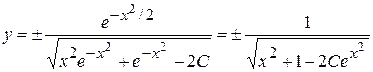

Ответ: 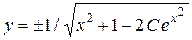- общее решение; 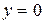- особое решение.

Тема 4: Дифференциальные уравнения второго и высших порядков.