1.
 |
Пусть x распределена по закону Бернулли с параметром р. Напомним, что таблица распределения выглядит так:
 | 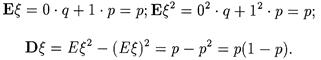 |
По определению математического ожидания и дисперсии дискретной случайной величины получаем
2. Пусть x распределена по биномиальному закону с параметрами п и р. Рассмотрим случайные величины
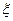
| … | n | ||
| p | P0 | P1 | … | Pn |
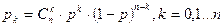
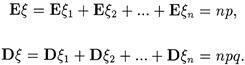 |
т.е. (xi — независимые случайные величины, распределенные по закону Бернулли. Тогда x можно представить в виде x = x 1 + x 2 +... + xn; и по следствию свойства 3 математического ожидания и свойства 4 дисперсии получаем:
3.
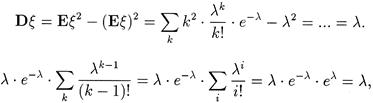 |
Пусть x распределена по закону Пуассона с параметром l, l > 0.
4. Пусть x распределена по геометрическому закону с параметрам q, 0<q<1. Тогда:
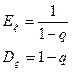
5.
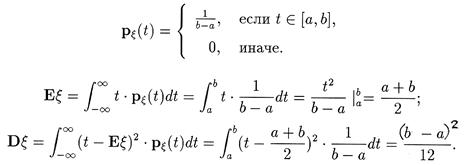 |
Пусть x распределена равномерно на интервале [ а, b ]. Напомним вид плотности распределения и вычислим:
6. Пусть x распределена по нормальному закону с параметрами а и s2. Напомним вид плотности распределения и вычислим: 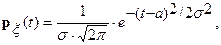
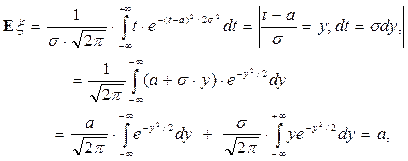
поскольку
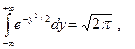
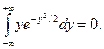
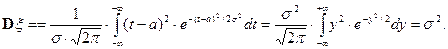
 2014-02-18
2014-02-18 982
982








