Дифференцируя или интегрируя известные разложения в ряд Тейлора, можно получить разложения новых функций в степенные ряды. Так; например, интегрируя фомулу геометрической прогрессии:
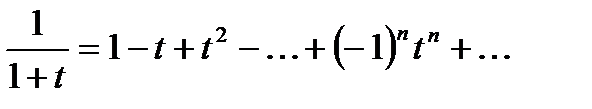
В пределах от 0 до х ( <1) равномерно сходится на отрезке с концами в точке 0 и х при
<1) равномерно сходится на отрезке с концами в точке 0 и х при  <1, получаем известную формулу (§5,формула 20.18, Лекция 20):
<1, получаем известную формулу (§5,формула 20.18, Лекция 20):
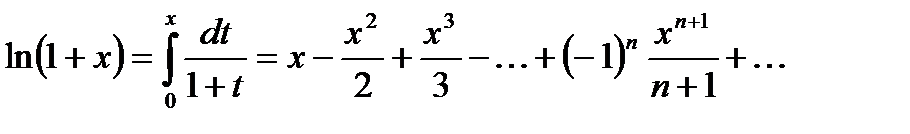
Раньше эта формула была доказана на полуинтервале 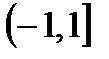 , а теперь только для интервала (-1,1). Однако, в силу второй теоремы Абеля о степенных рядах из справедливости формулы:
, а теперь только для интервала (-1,1). Однако, в силу второй теоремы Абеля о степенных рядах из справедливости формулы:
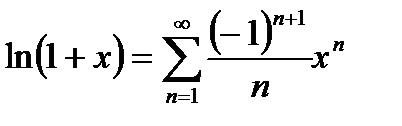
На интервале (-1,1) сразу следует ее справедливости и при х=1. В результате дифференцирования или интегрирования заданного степенного ряда иногда удается получить ряд, сумма котрого уже известна: это позволяет вычислить и сумму исходного степенного ряда.
Пример 21.1. Найти разложение функции arcsin x в ряд Тейлора
Заметим, что (arcsin x)’ = 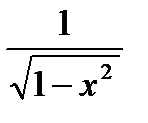
Разложим (arcsin x)’ в ряд по формуле разложения степени бинома:
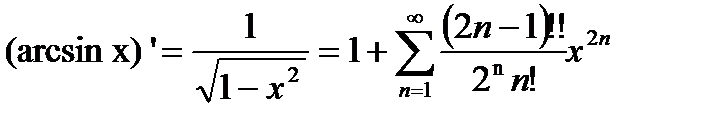 (21.7)
(21.7)
Радиус сходимости получившегося ряда равен единице, интегрируя ряд (21.7) от 0 до х,  <1.получим
<1.получим
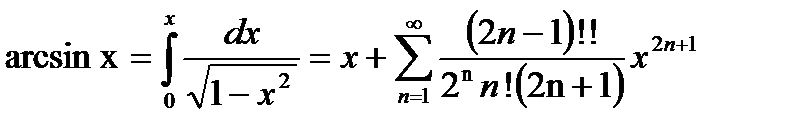
Пример 21.2. Разложим функцию arctg x в степенной ряд и с помощью него найдем числовой ряд, сумма которого равна 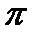 .
.
Поступая при  <1 аналогично примеру 1, имеем:
<1 аналогично примеру 1, имеем:
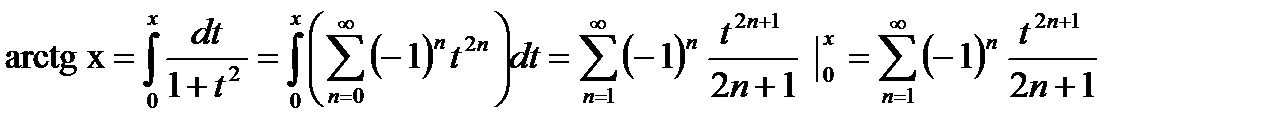 (21.8)
(21.8)
Заметим, что полученный ряд при х=±1, поэтому согласно второй теореме Абеля для степенных рядов, сумма ряда являясь непрерывной функцией на отрезке 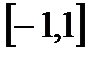 , и совпадает с arctg x на интервале (-1,1). Совпадает с ним и в концевых точках х=±1. Иначе говоря, разложение справедливо для отрезка
, и совпадает с arctg x на интервале (-1,1). Совпадает с ним и в концевых точках х=±1. Иначе говоря, разложение справедливо для отрезка 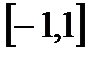 .
.
Взяв в этом разложении х=1, и заметив, что arctg 1= 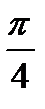 , получим:
, получим:
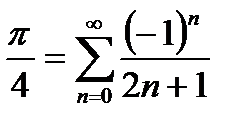
Полученный ряд называется рядом Лейбница
Пример 21.3. Найдем сумму ряда
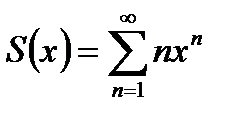 (21.9)
(21.9)
Радиус сходимости этого ряда равен 1. Согласно признаку Даламбера:
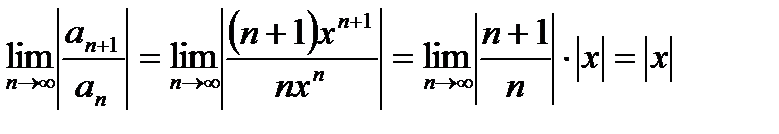 ,
,
Следовательно, ряд сходится абсолютно при 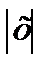 <1 и при
<1 и при 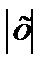 >1 расходится.
>1 расходится.
Из (21.9) следует, что:
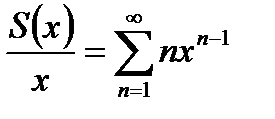
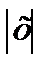 <1
<1
Проинтегрируем этот ряд почтенно от 0 до х, 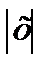 <1
<1
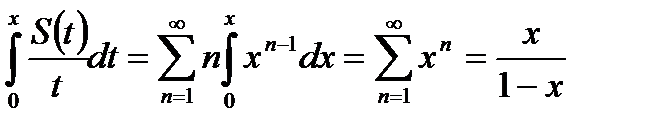
И затем продифференцируем получившееся тождество:
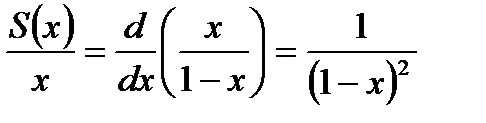
В результате получаем:
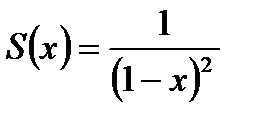
 <1
<1
Пример 21.4. При разложении рациональных функций в ряд Тейлора удобно использовать их разложение на элементарные дроби. Поясним этот метод на примере. Найдем разложение функции:
ƒ 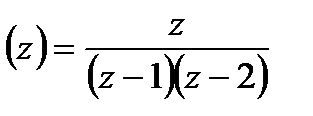
В ряд Тейлора в окрестностях точек 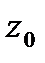 =0,
=0, 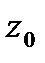 =
= 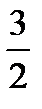 и
и 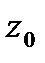 = 4.
= 4.
Разложив функцию ƒ(z) на элементарные дроби, получим:
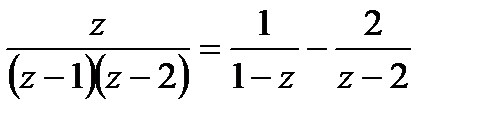
Найдем сначала ряд Тейлора в окрестности 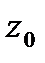 =0.
=0.
Для этого заметим, что дроби:
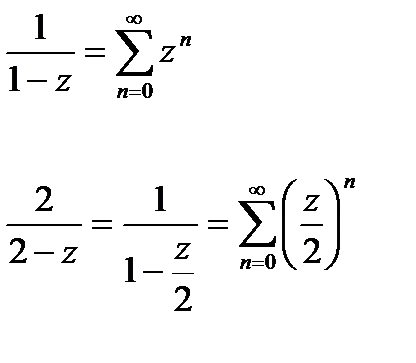
Со знаменателями z, 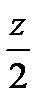 при условии, что
при условии, что 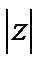 <1 и соответственно, что
<1 и соответственно, что  <1. Таким образом,
<1. Таким образом,
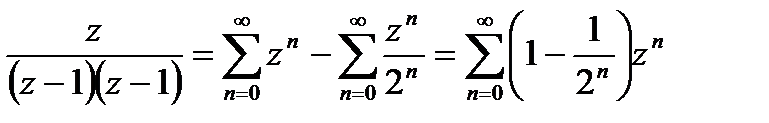 ,
, 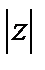 <1
<1
Рассмотрим точку 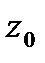 =
= 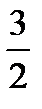 . Для получения ряда Тейлора функции ƒ
. Для получения ряда Тейлора функции ƒ 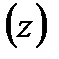 в окрестности точки
в окрестности точки 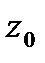 =
= 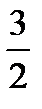 снова воспользуемся суммой бесконечно убывающей геометрической прогрессии, но проделаем это иначе, выделяя в знаменателе элементарные дроби, на которые разложена дробь ƒ
снова воспользуемся суммой бесконечно убывающей геометрической прогрессии, но проделаем это иначе, выделяя в знаменателе элементарные дроби, на которые разложена дробь ƒ 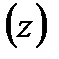 , члены
, члены 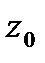 =
= 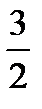 .
.
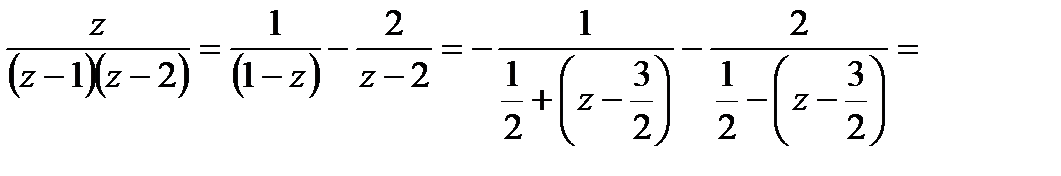
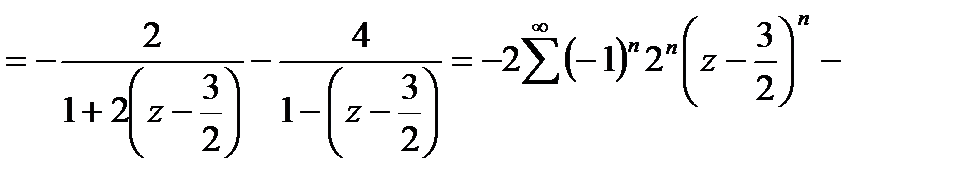
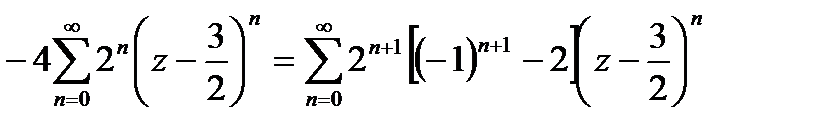
Эта выкладка справедлива при условии, что 2 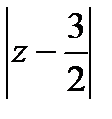 <1, то есть если
<1, то есть если 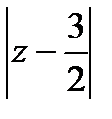 <
< 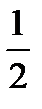 . Радиус сходимости получившегося ряда равен
. Радиус сходимости получившегося ряда равен 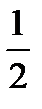 .
.
Рассмотрим точку 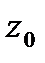 =4. Имеем:
=4. Имеем:
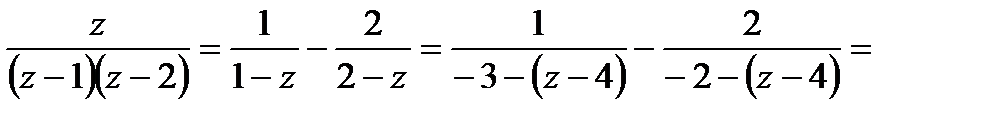
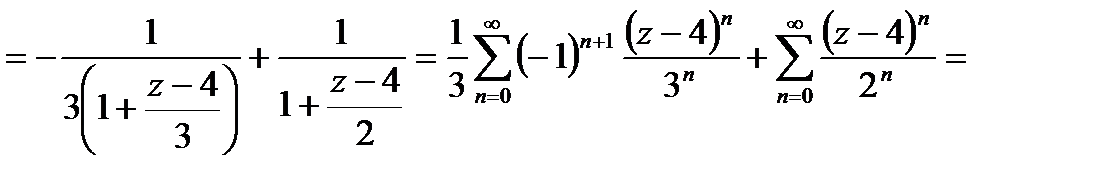
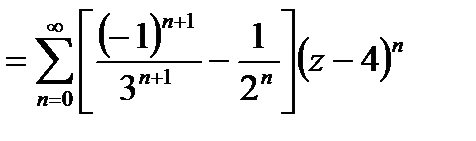
Все это справедливо, когда 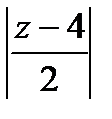 <1, то есть при
<1, то есть при 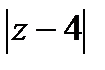 <2. Отсюда, как и выше, следует, что радиус сходимости получившегося ряда равен 2.
<2. Отсюда, как и выше, следует, что радиус сходимости получившегося ряда равен 2.
Пример 21.5. Найдем сумму ряда
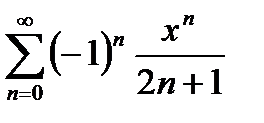 (21.10)
(21.10)
в области его сходимости. При 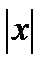 <1 этот ряд сходится абсолютно, ибо
<1 этот ряд сходится абсолютно, ибо
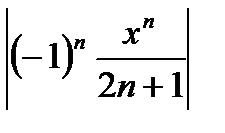
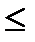
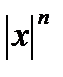
При 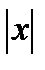 >1 он расходится, так как его общий член не стремится к нулю, при х=1 он сходится по признику Лейбница, при х=-1 расходится, что например,следует, согласно интегральному признаку сходимости видов из сходимости интеграла
>1 он расходится, так как его общий член не стремится к нулю, при х=1 он сходится по признику Лейбница, при х=-1 расходится, что например,следует, согласно интегральному признаку сходимости видов из сходимости интеграла
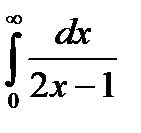
Заметим, что
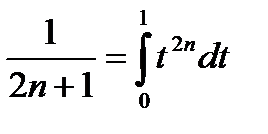
И преобразуем ряд (21.10) следующим образом:
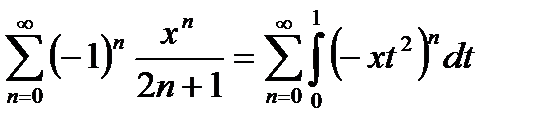 (21.11)
(21.11)
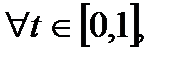 выполняется неравенство
выполняется неравенство 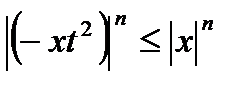
Поэтому, если 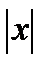 <1, то по признаку Вейерштрасса ряд
<1, то по признаку Вейерштрасса ряд
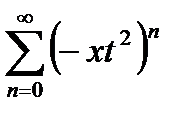 (21.12)
(21.12)
Равномерно сходится (по t) на отрезке 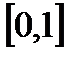 , следовательно, его можно почленно интегрировать.
, следовательно, его можно почленно интегрировать.
Его можно почленно интегрировать и при х=1, хотя в этом случае ряд 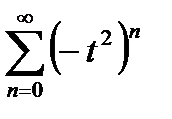 не сходится равномерно на отрезке
не сходится равномерно на отрезке 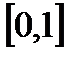 , так как он даже расходится при t=1. Возможность почленного дифференцирования ряда (21.12) при х=1 можно проверить, например, непосредственно
, так как он даже расходится при t=1. Возможность почленного дифференцирования ряда (21.12) при х=1 можно проверить, например, непосредственно
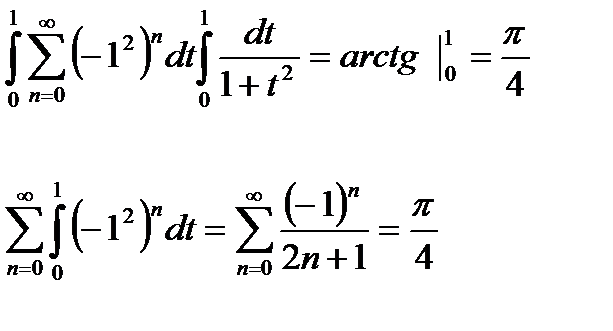
Итак,  (-1,+1) имеем:
(-1,+1) имеем:
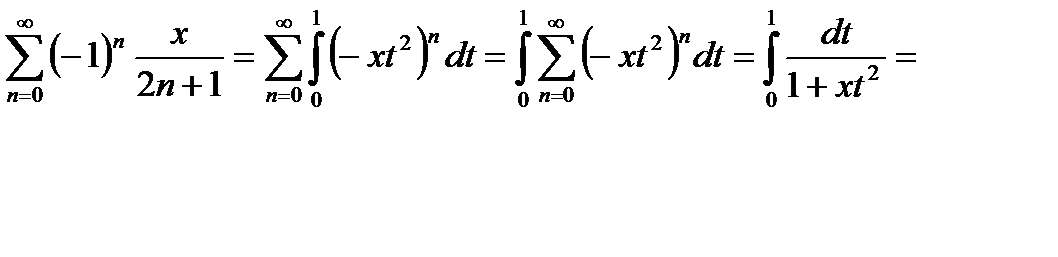
Если 0<х<1
= 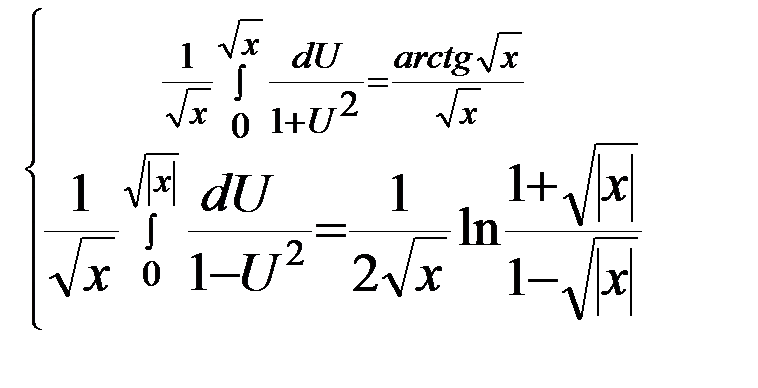 Если х=0
Если х=0
Если -1<х<0
 2015-03-07
2015-03-07 6510
6510