Продольные волны могут распространяться как в твердых телах, так и в жидкостях или газах. Пример продольных волн - звуковые волны в жидкостях и газах. Они представляют собой колебания давления, распространяющиеся в этих средах.
Волновой процесс. Понятие волнового фронта.
МЕХАНИЧЕСКИЕ ВОЛНЫ В УПРУГОЙ СРЕДЕ
ЛЕКЦИЯ 9
Тело, колеблющееся в упругой среде, периодически воздействует на прилегающие к нему частицы среды, выводя их из положений равновесия и заставляя совершать вынужденные колебания, возмущающие частицы среды..
Механические возмущения (деформации), распространяющиеся в упругой среде, называются упругими волнами.
Геометрическое место точек среды, в которых фаза колебаний частиц одинакова, называется волновым фронтом или волновой поверхностью. Например, существуют сферические волны, исходящие от точечного источника колебаний, волновая поверхность которых представляет собой сферу.
Упругая волна называется продольной, если колебания частиц среды происходят в направлении распространения волны. Если же частицы среды колеблются в плоскостях, перпендикулярных направлению распространения волны, то такая волна называется поперечной.
|
|
|
Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Поэтому поперечные волны могут существовать лишь в твердых телах. Таковы, например, волны, распространяющиеся вдоль струн музыкальных инструментов.
В отличие от других видов механического движения среды (например, ее течения) распространение упругих волн в среде не связано с переносом вещества.
Частицы, отстоящие друг от друга на расстоянии u T (u ‑ скорость распространения, T – период колебаний), колеблются в одинаковой фазе. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l.
l = u T или u =λν,
где n ‑ частота колебаний.
Рассмотрим распространение продольной волны в тонком упругом стержне, которая создается источником колебаний, расположенном в некоторой точке пространства (x = 0). Выделим объем стержня длиной Δ x (рис.9.1).. Под действием упругих сил, возникающих в точках x и x +Δ x, рассматриваемыйобъембудет испытывать деформации растяжения и сжатия.
Пусть s - упругое смещение границ выделенного объема от положений равновесия. Применение к данному объему закона движения центра масс приводит к дифференциальному уравнению
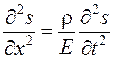 , (9.1)
, (9.1)
где t –время, ρ –плотность материала стержня, E – модуль Юнга.
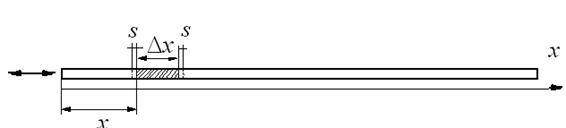
Рис.9.1
Уравнение (9.1) называется дифференциальным волновым уравнением, котороезаписано в одномерном виде.
|
|
|
Решение уравнения (9.1) для волны, распространяющейся в направлении оси x, имеет вид:
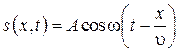 , (9.2)
, (9.2)
где A – амплитуда колебаний частиц среды (амплитуда волны); w – циклическая частота колебаний источника, которая равна частоте колебаний частиц среды, вызванных волной.
Можно показать, что данное уравнение имеет общий характер,. В трехмерном виде волновое уравнение имеет следующий вид:
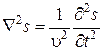 , (9.3)
, (9.3)
где Ñ2 ‑ оператор Лапласа:
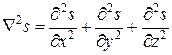 .
.
Решением этого уравнения является смещение s частиц среды от положений равновесия, как функция координат и времени. s = s (x,y,z, t).
Определим смысл величины u в уравнениях (9.2) и (9.3), имеющей размерность скорости. Зафиксируем какое-либо значение фазы, в уравнении (9.2), положив
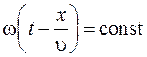 . (9.4)
. (9.4)
Выражение (9.4) описывает распространение волнового фронта. Продифференцировав (9.4), получим
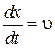 . (9.5)
. (9.5)
Скорость распространения волны u в приведенных выше уравнениях есть скорость перемещения фазы, поэтому эту скорость называют фазовой скоростью.
Из уравнения (9.1) следует
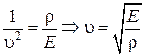 .
.
Т.е.фазовая скорость продольных волн в твердых телах зависит от модуля Юнга E и плотности среды r.
Можно показать, что скорость поперечных волн определяется модулем сдвига:
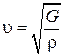 .
.
Скорость волн в идеальном газе для адиабатического процесса распространения зависит от абсолютной температуры:
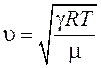 ,
,
где γ – показатель адиабаты (отношение изобарной и изохорной теплоемкостей газа, γ= сp/сV), R – универсальная газовая постоянная, T - абсолютная температура, μ – молярная масса газа.
Функция (9.2) описывает плоскую волну, так как волновой фронт представляет собой плоскость.
Уравнение плоской волны можно представить в симметричном виде относительно t и х. Для этого вводится понятие волнового числа k:
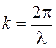 . (9.6)
. (9.6)
Используя (9.7), получим выражение для скорости u:
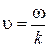 . (9.7)
. (9.7)
Тогда уравнение волны описывается соотношением
s = A cos(w t – kx). (9.8)
Если волну рассматривать на расстоянии значительно большем, чем размеры источника, то источник можно считать точечным. В этом случае в изотропной среде волна будет сферической. Такую волну описывает решение дифференциального уравнения (9.3), представленное в сферических координатах. Уравнение сферической волны имеет вид:
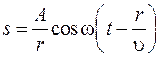 . (9.9)
. (9.9)
Из (9.9) видно, что амплитуда сферической волны изменяется обратно пропорционально расстоянию от волнового фронта до источника.
Зависимость амплитуды волны от расстояния обусловлено тем, что по мере удаления фронта волны от источника за равные промежутки времени в колебательное движение вовлекаются все возрастающие объемы среды.
 2014-02-18
2014-02-18 8161
8161
