Аппроксимация – замена одних математических объектов другими в том или ином смысле близкими к исходным.
Под аппроксимацией в математике понимается операция нахождения неизвестных численных значений какой-либо величины по известным ее значениям и, может быть, численных значений других величин, связанных с рассматриваемой. Задачи такого рода возникают во многих разделах науки и ее приложений, и проблема аппроксимации поэтому является многосторонней. Одной из основных задач аппроксимации является задача интерполяции. В достаточно общем виде для многих случаев, она может быть сформулирована следующим образом. Пусть в 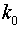 точках
точках 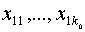 известны значения функции
известны значения функции 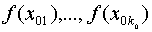 ; в
; в 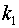 точках
точках 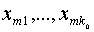 известны значения первой производной от нее
известны значения первой производной от нее 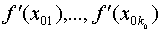 и т.д. и, наконец, в
и т.д. и, наконец, в 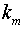 точках
точках 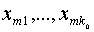 известны значения ее m–ой производной
известны значения ее m–ой производной 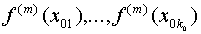 . Точки
. Точки 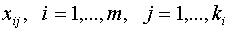 – называются узлами интерполирования., а совокупность пар чисел
– называются узлами интерполирования., а совокупность пар чисел 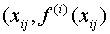 – исходными данными интерполирования. Общее число исходных данных
– исходными данными интерполирования. Общее число исходных данных 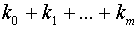 n.
n.
Пусть значение x отлично от узлов 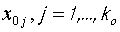 , где известны значения f. Нужно, пользуясь исходными данными, найти значение f(x), или значение производной
, где известны значения f. Нужно, пользуясь исходными данными, найти значение f(x), или значение производной 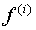 или других величин, связанных с f.
или других величин, связанных с f.
Если относительно f не делать дополнительных предположений, то такая задача является неопределенной, и в качестве f(x) может быть взято любое число. Для пояснения существа вопроса достаточно взять простейший частный случай, когда интерполирование f(x) для всех значений [a,b] выполняется по значениям только функции f, заданных в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений в каком-либо натуральном эксперименте, либо в результате вычисления по некоторой модели при подмене сложной модели более простой, Поэтому требуется найти достаточно простую формулу, которая позволила бы найти приближенное значение функции с требуемой точностью в любой точке отрезка, в результате ставится следующая задача.
Пусть на отрезке [a,b] задана сетка 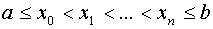 и в ее узлах заданы значения f(x):
и в ее узлах заданы значения f(x): 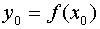 ,
, 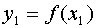 ,…,
,…,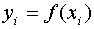 ,…,
,…,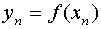 . Пусть на [a,b] задано также некоторое семейство функций
. Пусть на [a,b] задано также некоторое семейство функций 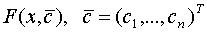 вектор параметров, значение которого определяет конкретную функцию из этого семейства. Требуется определить значения свободных параметров
вектор параметров, значение которого определяет конкретную функцию из этого семейства. Требуется определить значения свободных параметров 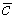 так, чтобы аппроксимирующая функция (интерполента)
так, чтобы аппроксимирующая функция (интерполента) 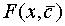 совпадала с f(x) в узлах сетки:
совпадала с f(x) в узлах сетки: 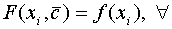 i=0,1,…,n.
i=0,1,…,n.
Основная цель интерполяции: получить быстрый (экономичный) алгоритм приближенного вычисления значений f(x) для значений x не содержащихся в таблице данных. Основной вопрос: как выбрать семейство функций 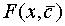 среди которых ищется интерполента и как оценить погрешность
среди которых ищется интерполента и как оценить погрешность 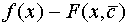 . Как правило, интерполирующие функции строятся в виде линейных комбинаций некоторых фиксированных функций:
. Как правило, интерполирующие функции строятся в виде линейных комбинаций некоторых фиксированных функций:
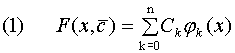
где 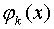 , k=0,1,…,n – фиксированная система функций. При этом задача интерполяции функции f(x) системой функций
, k=0,1,…,n – фиксированная система функций. При этом задача интерполяции функции f(x) системой функций 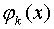 на сетке состоит в нахождении коэффициентов C0,…,Cn, для которых выполнены условия, называемые условиями интерполирования:
на сетке состоит в нахождении коэффициентов C0,…,Cn, для которых выполнены условия, называемые условиями интерполирования:
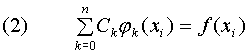
или в развернутом виде:
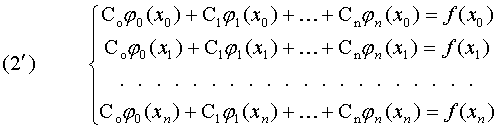
Возникает вопрос о существовании и единственности решения общей задачи интерполирования. Для того чтобы система имела единственное решение, необходимо и достаточно чтобы определитель матрицы был отличен от нуля.

Более того поскольку узлы 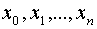 могут быть расположены на [a,b] как угодно, лишь бы среди них не было совпадающих, необходимо потребовать, чтобы
могут быть расположены на [a,b] как угодно, лишь бы среди них не было совпадающих, необходимо потребовать, чтобы 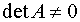 при любом расположении узлов. Выполнение или невыполнение этого требования зависит от выбора системы функций
при любом расположении узлов. Выполнение или невыполнение этого требования зависит от выбора системы функций 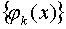 , k=0,…,n.
, k=0,…,n.
Система функций 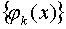 , k=0,…,n называется системой Чебышева на [a,b], если определитель матрицы A отличен от нуля при любом расположении узлов
, k=0,…,n называется системой Чебышева на [a,b], если определитель матрицы A отличен от нуля при любом расположении узлов 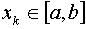 , когда среди этих узлов нет совпадающих. Таким образом, общая задача интерполирования однозначно разрешима, если
, когда среди этих узлов нет совпадающих. Таким образом, общая задача интерполирования однозначно разрешима, если 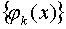 , k=0,…,n чебышевская система функций. Функция
, k=0,…,n чебышевская система функций. Функция 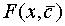 (1) удовлетворяющая условиям интерполяции (2), называется обобщенным интерполяционным многочленом по системе
(1) удовлетворяющая условиям интерполяции (2), называется обобщенным интерполяционным многочленом по системе 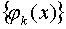 , k=0,…,n.
, k=0,…,n.
Примеры чебышевских систем:
система степенных функций: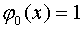 ,
, 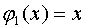 ,
, 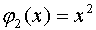 ,
, 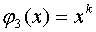 .
.
система тригонометрических функций на отрезке периодичности: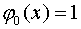 ,
,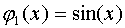
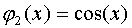 ,
, 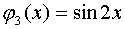 ,
, 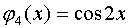 ,…
,…
 2014-02-09
2014-02-09 3491
3491








