Пусть на [-1,1] задана система функций 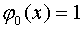 ;
;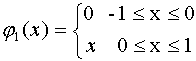 . Тогда, если в качестве узлов взять, например, точки
. Тогда, если в качестве узлов взять, например, точки 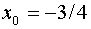 ;
;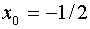 ; то получим
; то получим 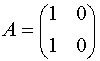 ,
,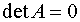 .
.
Другой пример: 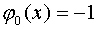 ;
; 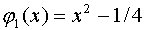 ;
; 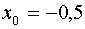 ;
; 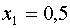 ;
; 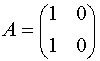 .
.
Вообще из (3) видно, что если какая-либо из функций 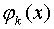 , k=0,…,n обращается на отрезке [a,b] в ноль более чем n раз, то система не является чебышевской. Действительно, если, например,
, k=0,…,n обращается на отрезке [a,b] в ноль более чем n раз, то система не является чебышевской. Действительно, если, например, 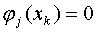 для некоторого j и для k=0,…,n, то выбирая точки
для некоторого j и для k=0,…,n, то выбирая точки 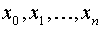 в качестве узлов интерполирования, получим, что j-ый столбец матрицы A содержит только нулевые элементы.
в качестве узлов интерполирования, получим, что j-ый столбец матрицы A содержит только нулевые элементы.
Отсюда можно доказать, что для того чтобы система 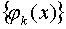 , k=0,…,n была чебышевской на [a,b], необходимо и достаточно, чтобы любой обобщенный интеграл по этой системе
, k=0,…,n была чебышевской на [a,b], необходимо и достаточно, чтобы любой обобщенный интеграл по этой системе  , у которого хотя бы один из коэффициентов отличен от нуля, имел на [a,b] не более n нулей.
, у которого хотя бы один из коэффициентов отличен от нуля, имел на [a,b] не более n нулей.
Можно также доказать, что определитель A отличен 0 тогда, когда система базисных функций линейно независима на множестве узлов. Поэтому система функций называется чебышевской, если она независима на любом конечном множестве (n+1) точек на отрезке [a,b].
Напомним, что система функций 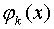 , k=0,…,n называется линейно зависимой на некотором множестве точек
, k=0,…,n называется линейно зависимой на некотором множестве точек 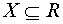 , если существует набор коэффициентов
, если существует набор коэффициентов 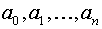 , среди которых хотя бы один отличен от нуля, обращающих в тождественный нуль на множестве X линейную комбинацию функций
, среди которых хотя бы один отличен от нуля, обращающих в тождественный нуль на множестве X линейную комбинацию функций 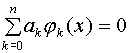 ,
, 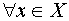 .
.
Если это равенство выполняется только в том случае, когда a0=a1=…=an=0, то система функций 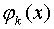 , k=0,…,n называется линейно зависимой на множестве X.
, k=0,…,n называется линейно зависимой на множестве X.
Очевидно, что система функций независима на множестве X, то она независима и на множестве 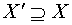 . Обратное неверно!
. Обратное неверно!
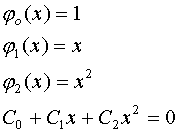 - линейно зависимы
- линейно зависимы
нельзя подобрать коэффициенты, чтобы многочлен є 0
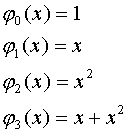 - линейно зависимы
- линейно зависимы
можно определить значения коэффициентов, чтобы значение многочлена є 0.
 2014-02-09
2014-02-09 967
967







