2014-02-18
1569
Теорема о конечном значении оригинала.
Теорема о начальном значении оригинала.
.
.
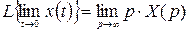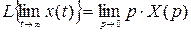Запишем дифференциальное уравнение одномерного объекта
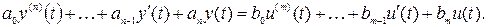(2.6)
Умножив все составляющие выражения (2.6) на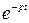 
и взяв интеграл по каждому слагаемому от 0 до +¥ и учитывая свойства преобразования Лапласа получим дифференциальное уравнение в операторной форме вида:
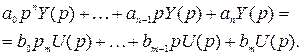(2.7)
Вынеся за скобки изображения Y(p) и U(p) получим уравнение вида:
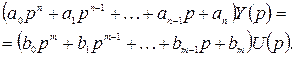(2.8)
Введем следующие обозначения:
;
.
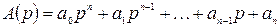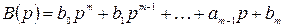Тогда уравнение (2.8) можно записать в виде:
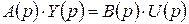. (2.9)
Откуда
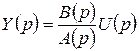. (2.10)
Введем обозначение:
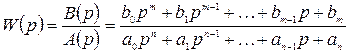. 2.11)
Тогда имеем, что
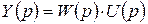. (2.12)
Функция W(p) называется передаточной функцией и представляет собой отношение изображения по Лапласу выходной переменной к изображению по Лапласу входной переменной при нулевых начальных условиях, т.е.
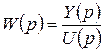. (2.13)
Формально передаточная функция получается из дифференциального уравнения путем замены в нем символов кратного дифференцирования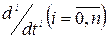 
на соответствующую степень 
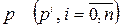и делением образованного таким образом многочлена правой части на многочлен левой части. Знаменатель передаточной функции (2.11) называется характеристическим полиномом, а приравненный нулю характеристическим уравнением. Коэффициенты полиномов являются вещественными величинами, определяемыми физическими параметрами системы.
