Классическое определение вероятности.
Вероятность есть число, характеризующее численную меру объективной возможности появления события в результате опыта.
Вероятностью события А называют отношение числа благоприятствующих этому событию элементарных исходов к общему числу элементарных исходов опыта.
Вероятность события А обозначают Р(А).
P(A) = 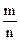 ,(1.1)
,(1.1)
где m – число благоприятствующих событию А исходов,
n – общее число возможных исходов опыта.
Соотношение (1.1) является классической формулой расчета вероятности событий, которые могут возникать в результате эксперимента с исходами, подпадающими под определение случаев.
Вероятность принимает значения от 0 до 1.
0 < Р (A) < 1
Вероятность невозможного события равна 0: Р(Ø)= 0,
вероятность достоверного события равна 1: Р(U) = 1.
Задача 1. Определить вероятность появления герба при одном броске монеты.
Опыт: бросок монеты.
Случайное событие А – появление герба при одном бросании.
Элементарные события: ω1 – выпадение герба (Г),
ω2 – выпадение цифры (Ц).
Возможные исходы опыта несовместные, равновозможные и образуют полную группу событий. n=2
Число благоприятствующих исходов ω1 (герб) равно 1. m=1.
P(A) – вероятность события А
P(A) =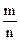 =
=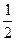 .
.
Задача 2. Определить вероятность того, что при бросании игральной кости выпадет не менее 5 очков.
Случайное событие А – выпадет не менее (³) 5 очков.
Элементарные события: ω1,. ω2, ω3, ω4, ω5,, ω6.
Исходы ω1,. ω2, ω3, ω4, ω5,, ω6.– несовместные, равновозможные, образуют полную группу. n=6.
Благоприятствующие исходы: ω5,, ω6. m=2.
P(A) =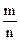 =
=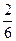 .
.
Задача 3. В урне имеется a белых и b черных шаров. Из урны наугад извлекли шар. Найти вероятность извлечения белого (событие А) и черного (событие В) шаров.
Число исходов опыта равно (a + b)
P(A) =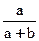 ,
,
P(B) =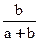 .
.
Задача 4. Из урны, содержащей 3 белых и 3 черных шара, извлекают 2 шара. Найти вероятность того, что они оба окажутся белыми.
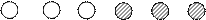 1 2 3 4 5 6
1 2 3 4 5 6
Благоприятствующие Не благоприятствующие
исходы: исходы:
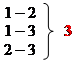

Число исходов n = 15 (несовместные, равновозможные и образуют полную группу)
Число благоприятствующих исходов m = 3
P(A) =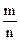 =
=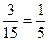 .
.
Задача 5. Из пяти букв разрезной азбуки составлено слово “КНИГА”. Ребенок, не умеющий читать, рассыпал буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово “КНИГА”.
В этом примере общее количество случаев определяется числом возможных перестановок букв, из которых состоит слово “КНИГА”, число это довольно внушительное и процедура прямого перебора в этом случае мало эффективна.
Задачами на отыскание количества комбинаций элементов, занимается раздел математики, называемый комбинаторикой.
Комбинаторика – это раздел математики, в котором изучаются количественные характеристики различных видов соединений элементов, независимо от природы самих элементов.
В основе комбинаторных методов лежат следующие два правила:
Правило сложения
Пусть k взаимоисключающих друг друга действия могут быть выполнены соответственно n 1, n 2,..., nk способами. Тогда какое-либо из действий можно выполнить n= n 1 + n 2 +... + nk способами.
Правило умножения
Пусть нужно последовательно выполнить k действий. Если первое действие можно выполнить n 1 способами, второе – n 2 способами,..., k -е – nk способами, тогда все k действий можно выполнить n способами.:
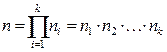 .
.
В комбинаторике различают три вида различных соединений (комбинаций) элементов произвольного множества:
– перестановки;
– размещения;
– сочетания.
Перестановками из m элементов называются такие их соединения, которые отличаются друг от друга порядком следования элементов.
| Pm = m! = 1 × 2 ×... × m. | (1.2) |
Пример 7. Составить все возможные перестановки из трех элементов {a, b, c}.
abc bac cab acb bca cba
P3 = 3!=1·2·3=6.
Размещениями из n элементов по m называют такие соединения m элементов, которые отличаются друг от друга хотя бы одним новым элементом или порядком их следования (m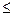 n).
n).
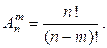 | (1.3) |
Пример 8. Составить все возможные размещения из трех элементов {a, b, c} по 2 элемента.
ab ac bc
ba ca cb.
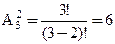
Сочетаниями из n элементов по m называют такие соединения m элементов, которые отличаются друг от друга хотя бы одним новым элементом, порядок следования элементов не учитывается (m 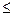 n).
n).
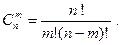 | (1.4) |
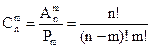 |
Пример 9. Составить все возможные сочетания из трех элементов {a, b, c} по 2 элемента.
 2014-02-18
2014-02-18 3850
3850