Определение 7.5

Таким образом, два и более событий на одном бесконечно малом участке произойти не могут.

Определение 7.4.

Случайный поток событий называется ординарным, если вероятность попадания двух и более событий на бесконечно малый участок Δ t несоизмеримо мала по сравнению с вероятностью попадания одного события на этот участок.

т.е. имеет место предел 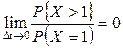. (7.6)

Случайный поток событий называется потоком без последействия, если вероятность попадания определенного числа событий на участок длиной Т не зависит от того, сколько событий попало на любой другой участок, не пересекающийся с ним.

Данное свойство потока говорит о том, что все последующие события в потоке не зависят от предыдущих.

Для простейшего потока событий случайная величина Х – количество событий попавших на интервал Т – распределена по закону Пуассона

(7.7)

где а = λТ – среднее число событий, попадающих на интервал Т (единственный параметр закона распределения);

λ – интенсивность наступления событий (количество событий в единицу времени);

Т – некоторый период времени.

Ряд распределения пуассоновской случайной величины имеет вид

xi			...	m	...
pi	е–а	а е–а	...	(а е–а)/m!	...

Доказательство формулы Пуассона (7.7).

Введем обозначения:

λ – интенсивность событий;

Т – заданный участок временной оси.

Разобьем участок длины Т на участки Δ t в количестве n.

Причем .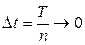

В силу стационарности и ординарности потока вероятность того, что на участке Δ t произойдет одно событие, определится следующим образом:

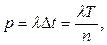
а вероятность того, что на участке Δ t не произойдет ни одного события:

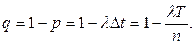
При условии 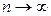вероятность 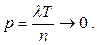Вероятность того, что за период времени Т произойдет ровно m событий можно рассматривать как вероятность появления m событий в n независимых испытаниях при 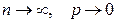, т.е. вычислять ее по формуле Бернулли:

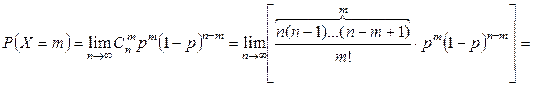
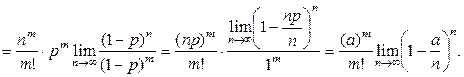
Поскольку = е^–а как замечательный предел, то

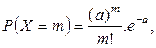
что и требовалось доказать.

Убедимся, что сумма вероятностей во второй строке ряда распределения равна единице, т.е. .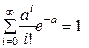

Для доказательства данного равенства преобразуем его левую часть: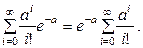

Здесь сумма 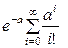представляет собой функциональный бесконечный ряд, сходящийся к функции е^а.

Преобразуем исходную сумму:

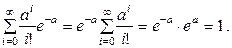
Таким образом, равенство 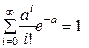доказано.