Определение 7.6

Равномерный закон распределения

Законы распределения непрерывных случайных величин.

Среди непрерывных случайных величин особого внимания заслуживают величины, имеющие один из следующих законов распределения:

1. равномерный;

2. показательный;

3. нормальный.

Непрерывная случайная величина распределена по равномерному закону, если ее плотность распределения имеет вид:

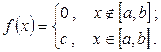(7.11)

Это распределение является непрерывным аналогом классического определения вероятности.

График плотности распределения для равномерно распределенной случайной величины имеет вид, показанный на рис.7.2.

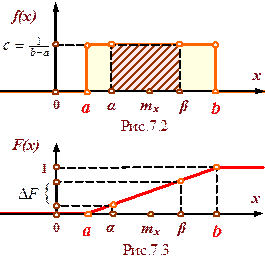
Найдем значение величины с в (7.11) с помощью первого свойства плотности распределения .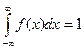

.

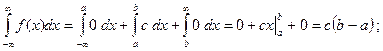
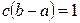Откуда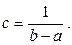

Тогда 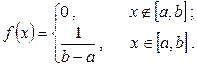(7.12)

Равномерный закон распределения имеет два параметра: а и b.

Интегральная функция распределения, согласно обратному преобразованию (5.2), определяется следующим образом:

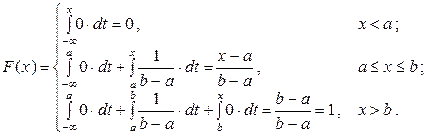
Таким образом, интегральная функция равномерно распределенной величины определяется как

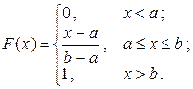(7.13)

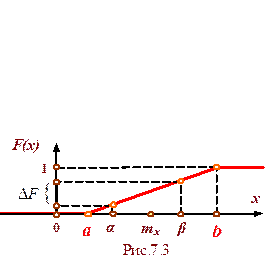
График интегральной функции для равномерно распределенной случайной величины имеет вид, показанный на рис.7.3.