Вероятность попадания случайной величины на заданный участок. Среднее квадратичное отклонение

Среднее квадратичное отклонение.

Дисперсия.

Математическое ожидание.

Числовые характеристики

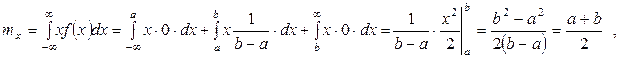
т.е. 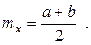(7.14)

Определим предварительно второй начальный момент

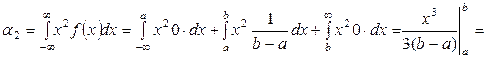
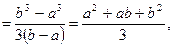
Дисперсию равномерно распределенной случайной величины определим по формуле связи:

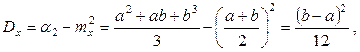
т.е. 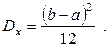(7.15)

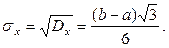(7.16)

Вероятность попадания равномерно распределенной случайной величины на заданный участок[ α,β ], если участок входит в диапазон [ a, b ], можно определить двумя способами:

1-й способ. По формуле (6.)

.

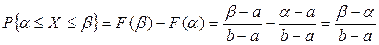2-й способ. По формуле (6.)

.

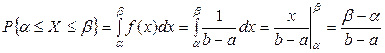Таким образом,

если 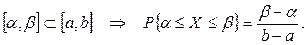(7.17)

Геометрически вероятности 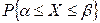соответствует область, выделенная штриховкой на рис.7.2.

Если участок [ α,β ] не входит в диапазон [ a,b ], то выражение (7.17) не является справедливым. В этом случае необходимо руководствоваться выражением

если (7.18)

где 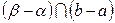– длина участка на числовой оси, являющегося пересечением для участка [ α,β ] и диапазона [ a,b ].