Выравнивание статистических рядов. Проверка статистических гипотез

Лекция №2.

1. Выравнивание статистичесих рядов.

Задача выравнивания (сглаживания) заключается в том, чтобы подобрать теоретическую плавную кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных. Эта кривая, с той или иной точки зрения наилучшим образом должна описывать данное статистическое распределение.

Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпирических функций, есть задача в значительной мере неопределенная, и решение ее зависит от того, что условиться считать «наилучшим». При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из сообрсжений, связанных с физикой решаемой задачи, с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Аналогично, при решении задачи выравнивания статистических рядов, прнципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения. Пусть для случайной величины Х мы построили гистограмму, которая имеет вид, приведенный на рисунке. Естественно предположить, что исследуемая случайная величина Х подчиняется нормальному закону:

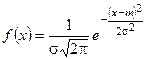
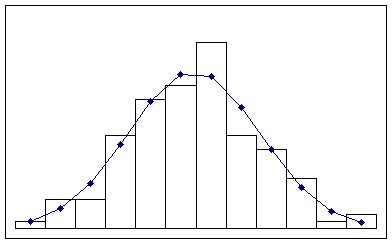
Тогда задача выравнивания переходит в задачу о рациональном выборе параметров m и σ.

Любая аналитическая функция с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределания:

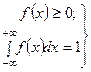
Предположим, что, исходя из тех или иных соображений, нами выбрана функция f(x), удовлетворяющая, приведенным выше условиям. С помощью этой функции мы хотим выровнять данное статистическое распределение; в выражение функции f(x) входит несколько параметров a, b, …; требуется подобрать эти параметры так, чтобы функция наилучшим образом описывала данный статистический материал. Один из методов, применяемых для решения этой задачи, – это так называемый метод моментов.

Согласно методу моментов, параметры a, b, … выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны сответствующим статистическим характеристикам. Например, если теоретическая кривая f(x) зависит только от двух параметров a и b, эти параметры выбираются так, чтобы математическое ожидание m_x и дисперсия D_x теоретического распределения совпадали с соответствующими статистическими характеристиками m_x* и D_x*. Если кривая f(x) зависит от трех параметров, можно подобрать их так, чтобы совпали первые три момента, и т. д.

При выравивании статистических рядов нерационально пользоваться моментами выше четвертого, так как точность вычисления моментов резко падает с увеличением их порядка.

2. Проверка гипотезы о согласованности теоретического и статистического распределения.

Допустим, что данное статистическое распределение выравнено с помощью некоторой теоретической кривой. Как бы хорошо ни была подобрана теоретическая кривая, между нею и теоретическим распределением низбежны некоторые расхождения. Возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат так называемые «критерии согласия».

Идея применения критериев согласия заключается в следующем.

Пусть на основании данного статистического материала необходимо проверить гипотезу Н, состоящую в том, что случайная величина Х подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: наприме, в виде функции распределения F(x) или в виде плотности распределения f(x), или же в виде совокупности вероятностей p_i, где p_i– вероятность того, что величина Х попадает в пределы i–го разряда.

Для того чтобы принять или опровергнуть гипотезу Н, рассмотрим некоторую величину U, характеризующую степень расхождения теоретического и статистическогораспределений. Величина может быть выбрана различными способами; например, в качестве U можно взять сумму квадратов отклонений теоретических вероятностей p_i от соответствующих частот p_i* или же сумму тех же квадратов с некоторыми коэффициентами («весами»), или же максимальное отклонение статистической функции распределения F*(x) от теоретической F(x) и т. д. Допустим, что величина U выбрана тем или иным способом. Очевидно, это есть некоторая случайная величина. Закон распределения этой случайной величины зависит от закона распределения случайной величины Х, над которой производились опыты, и от числа опытов n. Если гипотеза Н верна, то закон распределения величины U определяется законом распределения величины Х и числом n.

Допустим, что этот закон распределения нам известен. В результате данной серии опытов обнаружено, что выбранная нами мера расхождения U приняла некоторое значение u. Спрашивается, можно ли объяснить это случайными причинами или же это расхождение слишком велико и указывает на наличие существенной разницы между теоретическим и статистическим распределениями и, следовательно, на непригодность гипотезы Н? Для ответа на этот вопрос предположим, что гипотеза Н верна, и вычислим в этом предположении вероятность того, что за счет случайных причин, связанных с недостаточным объемом опытного материала, мера расхождения U окажется не меньше, чем наблюденное нами в опыте значение u, т. е. вычислим вероятность события:

U≥u

Если эта вероятность весьма мала, то гипотезу Н следует отвергнуть как мало правдоподобную; если же эта вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе Н.

Возникает вопрос о том, каким же способом следует выбирать меру расхождения U? Оказывается, что при некоторых способах ее выбора закон распределения величины U обладает весьма простыми свойствами и при достаточно большом n практически не зависит от функции F(x). Именно такими мерами расхождения и пльзуются в математической статистике в качесиве критериев согласия.

Одним из наиболее часто используемых критериев согласия является, так называемый, «критерий χ²» Пирсона.

Предположим, что произведено n независимых опытов, в каждом из которых случайная величина X приняла определенное зеачение. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда:

Ii	x1; x2	X2; x3	…	xk; xk+1
pi*	p1*	p2*	…	pk*

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина Х имет данный закон распределения (заданный функцией распределения F(x) или плотностью f(x)). Назовем этот закон распределения «теоретическим».

Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:

p₁, p₂,..., p_k.

Проверяя согласованность теоретического и статистического распределений, будем исходить из расхождения между теоретическими вероятностями p_i и наблюденными частотами p_i*. Естественно выбрать в качестве меры расхождения между теоретическим и статистическим распределениями сумму квадратов отклонений (p_i*-p_i), взятых с некоторыми «весами» c_i:

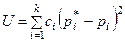
Коэффициенты c_i («веса» разрядов) вводятся потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Одно и то же по абсолютной величине отклонение (p_i*-p_i) может быть мало значительным, если сама вероятность p_i велика, и очень заметным, если она мала. Поэтому естественно «веса» c_i взять обратно пропорциональными вероятностям разрядов p_i.

К. Пирсон покзал, что если положить

,

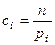то при больших n закон распределения величины U обладает весьма простыми свойсивами: он практически не зависит от функции распределения F(x) и от числа опытов n, а зависит только от числа разрядов k, а именно, этот закон при увеличении n прближается к так называемому «распределению χ²»

При таком выборе коэффициентов c_i мера расхождения обычно обозначается χ²:

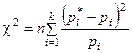
Распределение χ² зависит от параметра r, называемого числом «степеней свободы» распределения. Число «степеней свободы» r равно числу разрядов k минус число независимых условий («связей»), наложенных на частоты p_i*. Примерами таких условий могут быть

,

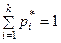если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);

,

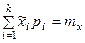если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статистическое средние значеия;

,

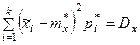если мы требуем, кроме того, совпадаения теоретической и статистической дисперсий и т. д.

Для распределения χ² составлены специальные таблицы. Фрагмент такой таблицы приведен ниже:

r	p
0,10	0,05	0,02
	13,36	15,51	18,17
	14,68	16,92	19,68
	15,99	18,31	21,20

В этой таблице входами являются: значение вероятности p и число степенй свободы r. Числа стоящие в таблице, представляют собой значения χ_z² для которых выполняется условие

,

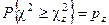где p_z– заданное значение p.

Схема применения критерия к оценке согласованности теоретического и статистического распределений сводится к следующему:

1) определяется мера расхождения χ²_набл по формуле

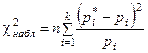
2) определяется число степеней свободы r как число разрядов k минус число наложенных связей s:

r=k – s

3) по r и заданному малому значению p по таблице определяется значение χ²_крит для которого справедливо

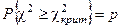
4) если 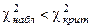то гипотезу можно признать как не противоречащей опытным данным, в противном случае гипотеза отбрасывается как неправдоподобная.

Насколько мала должна быть вероятность p для того, чтобы отбросить или пересмотреть гипотезу, – вопрс неопределенный; он не может быть решен из математических соображений, так же как и вопрос о том, насколько мала должна быть вероятность события для того, чтобы считать его практически невозможным. На практике, рекомендуется выбирать p≤0,1.