2014-02-09
371
Теорема 2.1. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Доказательство. 1) Необходимость. Пусть векторы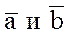 
ортогональны,j- угол между ними. Тогда cosj=0 и, в силу формулы (1), 
.
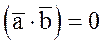2. Достаточность. Пусть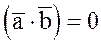 
. Докажем, что векторы 
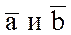ортогональны. Если хотя бы один из векторов 
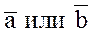является нулевым, то он ортогонален любому вектору.
Если же векторы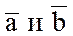 
ненулевые, то 
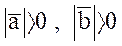, поэтому из равенства 
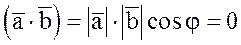вытекает, что cosj=0, т.е. векторы ортогональны, ч.т.д.
