Теорема 3.3. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их ВП.
Доказательство. 1). Необходимость вытекает из определения ВП.
2). Достаточность. Пусть 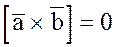 . Докажем, что векторы
. Докажем, что векторы 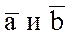 коллинеарны. Если хотя бы один из векторов
коллинеарны. Если хотя бы один из векторов 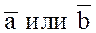 является нулевым, то он коллинеарен любому вектору.
является нулевым, то он коллинеарен любому вектору.
Если же оба вектора 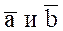 ненулевые, то
ненулевые, то 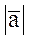 >0,
>0, 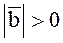 и поэтому из равенства
и поэтому из равенства 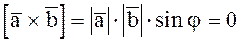 следует, что sinj=0, j=0, т.е. векторы
следует, что sinj=0, j=0, т.е. векторы 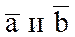 коллинеарны, ч.т.д.
коллинеарны, ч.т.д.
Заметим, что так как площадь параллелограмма равна произведению смежных сторон этого параллелограмма на синус угла между ними, то из определения ВП (пункт 1) получим, что длина (или модуль) ВП 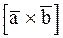 равняется площади параллелограмма, построенного на приведенных к общему началу векторах
равняется площади параллелограмма, построенного на приведенных к общему началу векторах 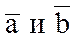 .
.
 2014-02-09
2014-02-09 572
572








