307
Выражение векторного произведения (ВП) в декартовых
Теорема.Если два вектора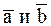 
определены своими ДПК
,
,
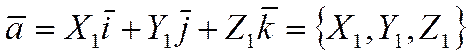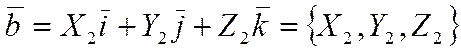то их ВП имеет вид
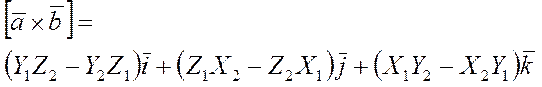. (1)
Для запоминания этой формулы удобно использовать символ определителя (см. предыдущий пункт) и переписать ее в виде
.
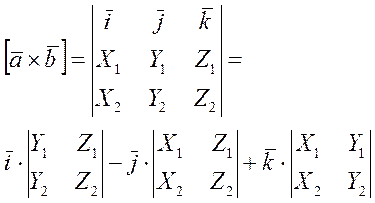Доказательство теоремы.Учитывая, что базисные векторы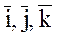 
взаимно ортогональны, образуют правую тройку 
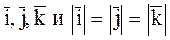, имеем 
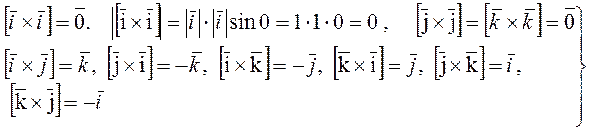(2)
Перемножая векторно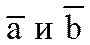 
, получим
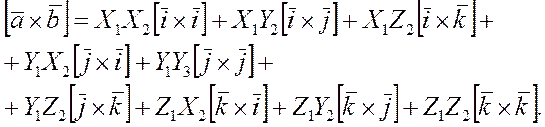
Из этого равенства и соотношений (2) получаем разложение (1).
Следствие.Если два вектора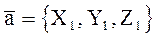 
и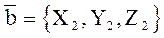 
коллинеарны, то их координаты пропорциональны:
.
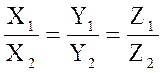Доказательство.Из равенства нулю векторного произведения и из формулы 1 имеем
,
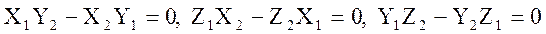ч.т.д.
