Пусть даны три вектора 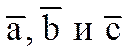 . Если вектор
. Если вектор 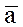 векторно умножается на вектор
векторно умножается на вектор 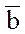 , а затем полученный вектор
, а затем полученный вектор 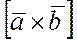 скалярно умножается на вектор
скалярно умножается на вектор 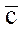 , то в результате получается число
, то в результате получается число 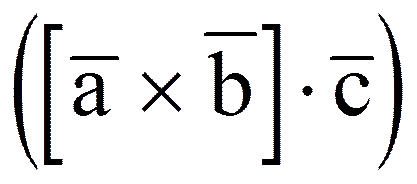 , называемое смешанным произведением векторов
, называемое смешанным произведением векторов 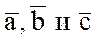 .
.
Из определения следует геометрический смысл смешанного произведения трех векторов:
Смешанное произведение 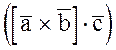 равно объему параллелепипеда, построенного на приведенных к общему началу векторах
равно объему параллелепипеда, построенного на приведенных к общему началу векторах 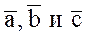 , взятому со знаком плюс, если тройка
, взятому со знаком плюс, если тройка 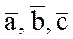 правая, и со знаком минус, если тройка
правая, и со знаком минус, если тройка 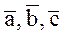 левая. Если же векторы компланарны, то
левая. Если же векторы компланарны, то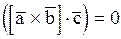 .
.
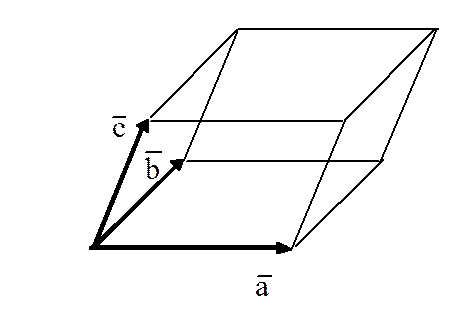
Отсюда видно, что 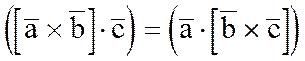 .
.
Поэтому можно записать смешанное произведение трех векторов 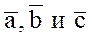 просто в виде
просто в виде
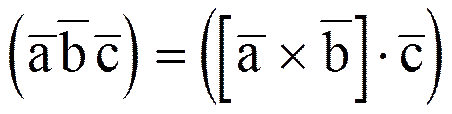 ,
,
не указывая, какие именно два вектора перемножаются векторно.
Следствие 1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанноно произведения.
Следствие 2. 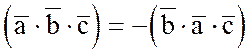 .
.
 2014-02-09
2014-02-09 546
546








