Выражение смешанного произведения в декартовых
Теорема. Если три вектора 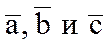 определены своими ДПК
определены своими ДПК
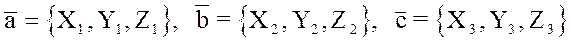 ,
,
то смешанное произведение 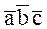 равно определителю, строки которого соответственно равны координатам перемножаемых векторов:
равно определителю, строки которого соответственно равны координатам перемножаемых векторов:
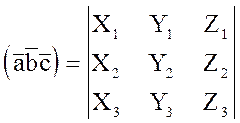
Доказательство. Т.к.
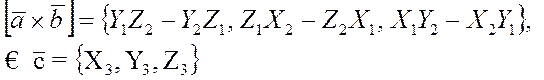 ,
,
то скалярное произведение этих векторов равно
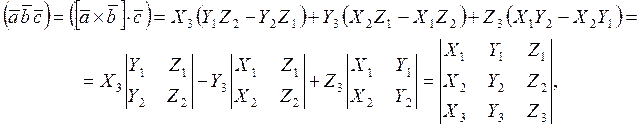
ч.т.д.
Следствие. Необходимым и достаточным условием компланарности трех векторов
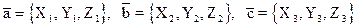 является равенство нулю определителя, строками которого являются координаты этих векторов:
является равенство нулю определителя, строками которого являются координаты этих векторов:
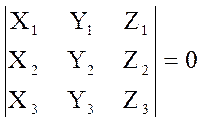 .
.
 2014-02-09
2014-02-09 339
339







