Задача Неймана
Сохраним уравнение
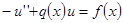 , но вместо условий Дирихле возьмем условия Неймана:
, но вместо условий Дирихле возьмем условия Неймана: 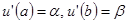 . Задача
. Задача

называется задачей Неймана для уравнения Гельмгольца.
Дискретизации здесь требует не только уравнение, но и граничные условия, для которых выберем простейший способ аппроксимации:
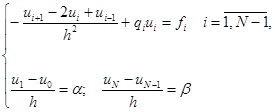
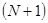 уравнений и
уравнений и 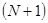 неизвестных.
неизвестных.
Матрица СЛАУ и вектор правой части соответственно имеют вид:
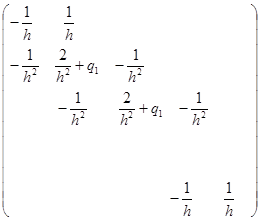

Матрица сохраняет трёхдиагональную структуру.
Рассмотрим подробнее уравнение СЛАУ:

Тут 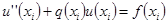 и
и 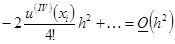 , т.е. уравнение имеет порядок аппроксимации
, т.е. уравнение имеет порядок аппроксимации 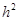 .
.

- граничные условия имеют порядок аппроксимации 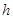 .
.
 2014-02-24
2014-02-24 607
607








