2014-02-24
1782
Глава 5 Элементы специальной теории относительности
Механический принцип относительности утверждает, что законы динамики одинаковы во всех инерциальных системах отсчета.
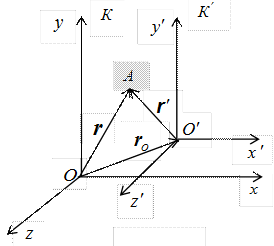
Рис. 5.1
Система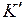 
движется относительно инерциальной системы К равномерно и прямолинейно со скоростью 
(
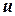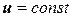). Скорость 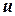направлена вдоль O
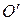. Тогда 
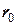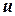=t.
Преобразования координат Галилея задают связь между радиусами-векторами или координатами произвольной точки A в обеих системах:
=
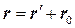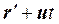или 
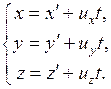(5.1)
Правило сложения скоростей в классической механике
Продифференцировав равенство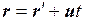 
по времени и учитывая, что в классической механике 
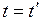, получаем
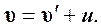(5.2)
Продифференцировав (5.2) по времени, получим соотношение для ускорений:
.
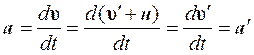Таким образом, имеем
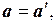(5.3)
т.е. система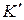 
инерциальна (точка A движется относительно ее равномерно). Это и есть доказательство механического принципа относительности.
Записанные соотношения (5.1)–(5.3) справедливы лишь в классической механике (u<< c), где с – скорость света в вакууме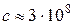 
м/с.
