Конспект лекций
В энергетике
В.Л. Вязигин
Вероятностно – статистические методы
Омск – 2007
Вязигин В.Л. Вероятностно-статистические методы в энергетике. Конспект лекций. – Омск: ГОУ ВПО ОмГТУ, 2006. – 55 с.
В конспекте изложены лекции, читаемые в Омском государственном техническом университете студентам 3-го курса специальности «Электроснабжение». В конспект вошли разделы, посвященные изучению случайных событий, способов задания законов распределение и характеристик случайных величин. Рассматриваются вопросы расчета надежности простейших логических схем, нахождения характеристик статистических распределений.
Конспект предназначен в первую очередь для дистанционной формы обучения, но может быть использован и студентами других форм обучения.
Конспект содержит 52 рисунка, 11 таблиц, 33 примера.
Редактор
ИД № от 2007
Подписано в печать. Формат 60 х 84 1/16. Бумага офсетная
Оперативный способ печати. Усл. печ. л. Уч.-изд. л.
Тираж 150 экз. Заказ
__________________________________________________________________
Издательство ОмГТУ. 644050, Омск - 50, пр. Мира, 11
Типография ОмГТУ
Дисциплина «Вероятностно-статистические методы в энергетике» изучается студентами специальности «Электроснабжение» в 5-м семестре. Программа предусматривает проведение 17 лекций, 8 практических занятий и выполнение 2-х индивидуальных заданий. Для выходного контроля знаний проводится экзамен.
Основу дисциплины составляют вопросы теории вероятностей и математической статистики. Их изучение позволит в дальнейшем (в других дисциплинах) познакомиться с методами планирования эксперимента, теорией массового обслуживания и теорией случайных функций, теорией надёжности.
Внимание, которое уделяется вероятностно-статистическим методам при подготовке инженеров-электриков, объясняется тем, что в современных системах электроснабжения (СЭС) постоянно протекают случайные процессы: включаются и отключаются отдельные электроприёмники, меняется потребляемая ими мощность в соответствии с нуждами потребителей, какие-то элементы СЭС выводятся в плановые ремонты, а какие-то отказывают аварийно, постоянно изменяются нагрузки линий электропередачи (ЛЭП) и трансформаторных подстанций (ТП), уровни напряжения и частоты.
Вследствие этого вероятностно-статистические методы применяются при решении ряда научных и технических задач в энергетике:
- анализ качества электрической энергии;
- определение расчётных электрических нагрузок;
- выбор параметров электрооборудования;
- выбор места расположения подстанций;
- постановка экспериментов и анализ их результатов;
- планирование стратегии технического обслуживания и ремонта оборудования.
Очень широко используются вероятностно-статистические методы в дисциплине «Надёжность электроснабжения», на истории становления которой остановимся несколько подробнее.
Теория надежности получила развитие в середине ХХ века. Толчком к этому послужило создание все более и более сложных и громоздких технических систем. Например, системы управления ракетами стали насчитывать миллионы элементов. Столь большое количество элементов приводит к тому, что ожидаемое время между отказами каких-либо из них начинает исчисляться минутами, а вся система не сможет функционировать безотказно без использования резервирования.
Развитие электроэнергетики привело к созданию крупных энергетических объединений, занимающих огромные территории (сотни тысяч квадратных километров). Системы электроснабжения некоторых промышленных предприятий насчитывают тысячи элементов.
До некоторых пор вопросам надёжности в энергетике внимание не уделялось. Толчком к их изучению послужила крупнейшая авария в объединенной канадо-американской энергосистеме девятого ноября 1965 г. В тот день из-за ложного срабатывания реле на линии электропередачи (ЛЭП), идущей от одной из гидростанций ниагарского каскада, всего за 11 минут была полностью обесточена территория сразу восьми штатов США и Канады с такими городами, как Нью-Йорк, Монреаль, Бостон и др. Авария случилась в 17:16, а восстановить электроснабжение удалось только в 7 часов утра. Последствиями явились не только огромные материальные убытки, но и гибель людей.
В настоящее время службы надёжности имеются в любых энергосистемах и системах электроснабжения крупных предприятий.
Изучение методов теории вероятностей полезно и с методологических позиций. Оно расширяет математическое образование, так как позволяет понять, что математика применяется не только для «конкретных задач». Создает научно обоснованную картину мира – фактически мы живем в мире случайных событий, случайных величин и процессов. Даже способствует формированию характера – многое, что нас ожидает, нельзя считать заранее предопределенным.
Глубинная основа этих явлений сформулирована в 1927 г. немецким физиком-теоретиком Вернером Гейзенбергом в форме, так называемого, «принципа неопределённости»: зная положение электрона в пространстве, мы никаким способом не можем определить направление его движения в дальнейшем.
Интересно, что случайный характер многих происходящих явлений, понимали многие выдающиеся деятели культуры. Так, например, Александр Дюма писал: «Случай играет в мире столь большую роль, что я стараюсь отводить ему как можно меньше места в уверенности, что и без моей помощи он позаботится о себе». Выдающийся французский астроном, физик, математик Пьер Симон Лаплас (1749-1827) в начале ХIХ века говорил, что «По большей части важнейшие жизненные вопросы являются на самом деле задачами из теории вероятностей».
Предмет теории вероятности. Краткая история её развития
Теория вероятности – это раздел математики, изучающий закономерности случайных явлений, то есть таких явлений, которые при повторении опыта протекают по иному.
В этом определении, на первый взгляд, заложен парадокс – как может быть закономерным случайное? Чтобы понять суть этого парадокса, необходимо иметь в виду два обстоятельства.
Во-первых, случайное явление не значит беспричинное явление. Для того чтобы появился тот или иной результат опыта, всегда имеются вполне определённые причины. Так, типичным примером случайного события считается подбрасывание монеты и падение её в результате цифрой или гербом вверх. Однако для того или иного результата есть вполне определённые причины. Если достоверно знать большое число исходных данных (массу и форму монеты, прилагаемое к монете усилие, его направление и точку приложения, плотность, температуру и степень неподвижности воздуха, уровень горизонтальности и качество обработки поверхности, на которую падает монета, и пр.), то можно было бы создать математическую модель, позволяющую предсказывать результат такого опыта. Но создание такой модели не имеет смысла, так как заранее невозможно предвидеть, как сложатся в каждом опыте эти меняющиеся в широком диапазоне исходные данные. Невозможность получения достоверной информации о начальных условиях делает явление в нашем понимании случайным.
Во-вторых, закономерности проявляются только в массовых случайных явлениях., т.е. явлениях многократно повторяющихся. Для подобных явлений характерно наличие, так называемой статистической устойчивости. Благодаря статистической устойчивости для массовых случайных явлений не возможно предсказание результата в одном отдельно взятом опыте, но зато возможно с достаточно большой степенью достоверности предвидеть результаты большой серии многократно повторяющихся опытов. Статистические закономерности массовых явлений проявляют себя в физике, химии, биологии, демографии и др. науках. Так, например, среди каждой тысячи новорожденных детей будет, как правило, 514 мальчиков.
Интересный пример проявления статистических закономерностей даёт наука о языке – лингвистика. Так, для любого языка характерна устойчивая повторяемость отдельных букв (таблицы частот повторения отдельных букв в русском языке можно найти во многих популярных книгах). Чаще всего в русскоязычном тексте встречается пробел между словами – 17,5%, буква «О» - 9,0%, реже всего – буква «ф» - 0,2%. Имея такую таблицу, можно без большого труда расшифровать простейший код, в котором вместо всем известных начертаний букв использованы другие значки. Достаточно только подсчитать частоту повторений этих значков (конечно, текст для дешифровки должен быть не слишком кратким).
Многие закономерности случайных явлений проявляются в азартных играх (по-арабски azar – игра в кости). Поэтому история развития теории вероятностей началась с решения задач из этой области людских интересов.
В 1494 г. итальянский преподаватель математики Лука Пачоли (1445-1514) сформулировал первую дошедшую до наших дней вероятностную задачу. Её называют «задачей о ставках». Условие задачи таково: два игрока играют на интерес в азартную игру с равными шансами на победу. Они договорились, что тот, кто достигнет определенного числа побед (обозначим это число буквой m), получает в награду ставки, поставленные на кон. Однако по каким-то причинам игрокам не удалось доиграть игру до конца – первый одержал a побед, а второй – b. Причем и a и b меньше m. Как поделить ставку? Пачоли предлагал делить их в пропорции a: b.
Прошло более 40 лет и другой знаменитый итальянец – математик и врач Джероламо Кардано (создатель карданного вала) раскритиковал это решение, но правильного предложить не смог. А найдено это решение было значительно позже – в 1654 г. Причем найдено путем переписки двух выдающихся французов: Блеза Паскаля (1623-1662), жившего в Париже, и Пьера Ферма (1601-1665), проживавшего в Тулузе. Они предложили следующее решение (рассмотрим его на частном примере, когда a = 1, b = 2, m = 3):
- если будет сыграна ещё одна игра, то с равными шансами победителем может оказаться любой игрок;
- при победе 1-го число побед сравняется и ставку надо поделить поровну;
- при победе 2-го b = m, и он заберёт всю ставку, тогда 1-му не достанется ничего;
- таким образом, 1-й игрок с равными шансами может получить или половину ставки или ничего, т.е. его выигрыш должен составлять 0,5(0,5+0) = 0,25 ставки;
- 2-й игрок с равными шансами может получить или половину или всю ставку, т.е. его выигрыш должен составлять 0,5(0,5+1) = 0,75 ставки.
В переписке Паскаля и Ферма (её после смерти Ферма опубликовал сын) были решены и другие знаменитые задачи зарождавшейся теории вероятностей. Эти задачи называют задачами шевалье Де Мере (1607-1648). Этот дворянин, поданный Людовика XIV не был простым кавалеристом («шевалье» – иначе «кавалер» - иначе «кавалерист»). Он был весьма образован, знал 6 языков, слыл известным моралистом. Чем он занимался в свободное от основной работы время в век, когда не было игровых автоматов, понятно из сформулированных им на основе собственного богатого опыта вопросов и задач. Эти задачи были связаны с игрой в кости.
Так, Де Мере заметил, что при бросании трёх игральных костей сумма равная 11 очкам почему-то наблюдается чаще, чем сумма в 12 очков, хотя число вариантов образования этих сумм кажется одинаковым:
- 11 очков можно получить при следующих шести сочетаниях очков на трёх костях: 6-4-1; 6-3-2; 5-5-1; 5-4-2; 5-3-3; 4-4-3.
- 12 очков можно получить тоже шестью способами: 6-5-1; 6-4-2; 6-3-3; 5-5-2; 5-4-3; 4-4-4.
Паскаль и Ферма пояснили, что на самом деле эти варианты появляются не одинаково часто. Вариант 5-4-3 (и другие с тремя разными числами) можно получить шестью способами (с учётом чисел, выпадающих на 1-й, 2-й и 3-й костях), вариант 6-3-3 (и другие с двумя повторяющимися числами) уже только тремя способами, а вариант 4-4-4 – одним единственным способом. Поэтому равновозможных вариантов появления суммы 11 больше, чем для суммы 12.
Паскаля и Ферма можно считать основоположниками теории вероятностей. Область интересов этих выдающихся людей была очень широкой. Блез Паскаль, прежде всего, известен как религиозный философ, физик и писатель. Его «Мысли» опубликованы в «Библиотеке мировой литературы». Пьер Ферма по профессии юрист, стал знаменит после того, как сын опубликовал его математические труды.
Первый математический трактат, в котором рассматривались вопросы теории вероятностей, был опубликован в 1657 г. Христианом Гюйгенсом, а 1-я книга, полностью посвящённая этим вопросам, называлась «Учение о случаях» и была издана в 1718 г. английским математиком французом по национальности Абрахамом де Муавром (1667-1754).
Основы современной элементарной теории вероятностей были изложены Пьером Симоном Лапласом в опубликованной в 1812 г. книге «Аналитическая теория вероятностей». Первый российский учебник по теории вероятностей был написан Виктором Яковлевичем Буняковским (1804-1889) в 1846 году и назывался «Основания математической теории вероятностей».
Если лидерство в развитии теории вероятностей на первых этапах принадлежало французам, то в дальнейшем большую роль в её развитии сыграли россияне – в ХIХ веке Пафнутий Львович Чебышёв (1821-1894), Андрей Андреевич Марков (1856-1922), Александр Михайлович Ляпунов (1857-1918), в середине ХХ века – Андрей Николаевич Колмогоров (1903-1987), который является основоположником современной «аксиоматической теории вероятностей».
Случайные события
Основные термины. Классификация случайных событий
В теории вероятности широко используются понятия событие и опыт.
Событие – это факт, который может иметь место в результате опыта. Иначе говоря, событие – это исход опыта, причем исход, который может произойти или не произойти.
Опыт (испытание, эксперимент) – это осуществление определенного комплекса условий.
Теория вероятностей рассматривает только такие опыты (а, следовательно, и их исходы), которые могут быть неоднократно воспроизведены, т.е. когда весь комплекс условий при проведении испытания может быть повторен заново. Если комплекс условий воспроизвести не удаётся, т. е. опыт может быть осуществлен только один раз, то появляющиеся в результате события называют н еопределенными (уникальными). Неопределённые события в теории вероятностей не рассматриваются. Так, например, опираясь на методы теории вероятностей невозможно достоверно предсказать результат очередного хоккейного матча (меняются условия опыта – составы команд, стадионы, зрители, судьи и пр.).
Все события подразделяются на три большие группы:
1). Достоверные - это такие события, которые в результате опыта произойдут обязательно. Например, если замкнуть исправную электрическую цепь, то по ней потечёт электрический ток
2). Невозможные - это такие события, которые при проведении опыта не произойдут никогда. Например, невозможен отказ сразу трёх трансформаторов на двухтрансформаторной ТП
3). Случайные - это такие события, о которых заранее нельзя сказать, произойдут они в результате опыта или нет. Например, в результате опыта – наблюдения за электродвигателем – он может находиться в работоспособном состоянии или в состоянии отказа
Наряду с достоверными и невозможными событиями принято различать, практически достоверные и практически невозможные. К таким событиям относятся события, шансы на появление (для невозможных) или не появление (для достоверных) которых хотя и существуют, но настолько пренебрежительно малы, что ими можно всегда пренебречь. Так, например, практически невозможным, хотя теоретически допустимым, событием является написание связного текста (стихотворения), если на клавиатуру персонального компьютера произвольно нажимает неграмотный ребёнок.. Практически достоверным событием является продолжительность жизни отдельного человека менее тысячи лет, хотя теоретически такую жизнь может прожить один из 10360 человек.
Следует подчеркнуть, что достоверность, невозможность или случайность событий сохраняют силу только в данном опыте, когда условия его проведения неизменны. Например, если замкнуть электрическую цепь, в которой отсутствует источник тока или напряжения, протекание в ней тока становится событием невозможным.
Для удобства отдельные события принято обозначать заглавными буквами. Например, фразу «трансформатор № 1 работоспособен» можно обозначить, как Rт1; фразу «в энергосистеме возник дефицит мощности» - как Д и т.п. Конечно же, применение этих обозначений не предполагает, что вместо букв могут быть подставлены какие-либо числа (как в алгебре). Применение букв вместо описания событий – это всего на всего сокращённая запись некоторых фраз.
Так как в дальнейшем будет рассматриваться ряд задач на анализ надёжности систем, кратко познакомимся с некоторыми терминами надёжности.
Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значение основных характеристик в заданных пределах. Термин «работоспособность » не следует отождествлять стермином «выполнение работы». Так, электрическая лампа будет работоспособна не только тогда, когда к ней подведено напряжение, и «горит свет», но и при отсутствии напряжения (в «режиме ожидания»).
Отказ (неработоспособность) – состояние объекта, при котором он не способен выполнять заданные функции.
Английский логик и математик Джон Венн (1834-1923) предложил наглядно изображать события в виде рисунков, которые получили название «диаграммы Венна».
 Диаграмма Венна (рис. 1) представляет собой квадрат со сторонами, равными единице. Событиям в этом квадрате соответствуют некоторые замкнутые области. Если «брошенная» произвольным образом в плоскость квадрата точка (исход опыта) попадает в замкнутую область, то считается, что событие произошло, если не попадет – событие не произошло. Термин «брошенная» подразумевает, что для точки задаются произвольные координаты в пределах от нуля до единицы, - это равнозначно тому, что по сторонам квадрата были бы установлены бортики, а брошенный внутрь шарик после многократных ударов об эти бортики занял произвольное заранее не прогнозируемое место в площади квадрата.
Диаграмма Венна (рис. 1) представляет собой квадрат со сторонами, равными единице. Событиям в этом квадрате соответствуют некоторые замкнутые области. Если «брошенная» произвольным образом в плоскость квадрата точка (исход опыта) попадает в замкнутую область, то считается, что событие произошло, если не попадет – событие не произошло. Термин «брошенная» подразумевает, что для точки задаются произвольные координаты в пределах от нуля до единицы, - это равнозначно тому, что по сторонам квадрата были бы установлены бортики, а брошенный внутрь шарик после многократных ударов об эти бортики занял произвольное заранее не прогнозируемое место в площади квадрата.
Среди возможных событий выделяют элементарные и сложные.
Под элементарными (простыми) событиями понимают непосредственные исходы опыта. Их нельзя разложить на другие события, и они взаимно исключают друг друга.
Сложные события могут быть при желании разбиты на элементарные.
Пример 1. Исходами опыта – наблюдения за состоянием однотрансформаторной подстанции в произвольный момент времени возможны следующие события:
А – трансформатор подстанции работоспособен;
В – трансформатор находится в состоянии отказа.
События А и В являются элементарными.
Пример 2 Исходами опыта – наблюдения за состоянием двухтрансформаторной подстанции в произвольный момент времени возможны следующие события (список не полный):
А - трансформатор №1 работоспособен, а трансформатор №2 – в состоянии отказа;
B - трансформатор №2 работоспособен, а трансформатор №1 – в состоянии отказа;
С - оба трансформатора в состоянии отказа;
D – оба трансформатора работоспособны;
E - отказ менее двух трансформаторов;
F - отказ хотя бы одного трансформатора;
RТ1 - трансформатор №1 работоспособен;
RТ2 - трансформатор №2 работоспособен.
В этом перечне событий элементарными являются события А, В, C и D. Все остальные – сложные. Например, событие RТ1 включает в себя события А и D.
Среди случайных событий могут быть выделены совместные и несовместные, зависимые и независимые, равно- и неравновозможные, противоположные. Остановимся подробнее на этих понятиях.
Совместными (несовместными) называются такие события, когда появление одного в единичном опыте не исключает (исключает) возможность появления другого.
Если любые два из группы событий несовместны между собой, то такую группу называют группой попарно-несовместных событий.
Например, в примере 1 события А и В несовместны.
В примере 2 события А, В, C и D попарно несовместны, события RТ1 и RТ2 – совместны.
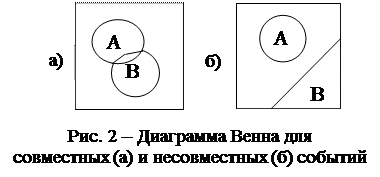 На диаграммах Венна совместные события (рис. 2-а) имеют общую зону, для несовместных событий (рис. 2-б) характерно отсутствие такой зоны..
На диаграммах Венна совместные события (рис. 2-а) имеют общую зону, для несовместных событий (рис. 2-б) характерно отсутствие такой зоны..
Зависимыми (независимыми) называются такие события, для которых появление одного влияет (не влияет) на возможность появления другого. Например, если электрическая нагрузка получает питание по двум включённым параллельно кабелям, то отказы кабелей являются зависимыми событиями, так как при отказе одного нагрузка на второй удваивается. Другим примером зависимых событий является замыкание на землю одной из фаз в сети с изолированной нейтралью трансформатора и двойное замыкание на землю в такой сети. Причиной этого является возрастание напряжения на двух неповрежденных фазах до линейного значения, если произошло замыкание любой из фаз на землю. Поэтому возможность замыкания на землю этих неповрежденных фаз возрастает.
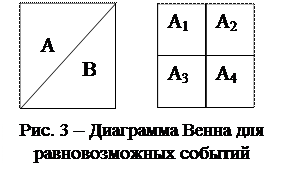
Равновозможными (симметричными) называются такие события, для которых нет объективных причин считать возможность появления одного события отличной от возможности появления другого или других. На диаграмме Венна (рис. 3) области таких событий занимают одинаковую площадь. Примерами равновозможных событий могут служить выпадение герба или цифры при однократном подбрасывании монеты, выпадение любой грани игральной кости и другие подобные примеры из области азартных игр. В реальной жизни равновозможные исходы опыта наблюдаются редко. Так, неравновозможными являются работоспособность и отказ объекта, включённое и отключенное состояние электродвигателей, работа кабельной ЛЭП с номинальной нагрузкой или в режимах перегрузки, недогрузки, холостого хода.

 Полной группой событий называется такой перечень несовместных событий, который исчерпывает все возможные результаты опыта. На диаграмме Венна (рис.4) зоны, соответствующие этим событиям, занимают всю площадь единичного квадрата.
Полной группой событий называется такой перечень несовместных событий, который исчерпывает все возможные результаты опыта. На диаграмме Венна (рис.4) зоны, соответствующие этим событиям, занимают всю площадь единичного квадрата.
Так, в примере 2 события А, В, C и D образуют полную группу, в том же примере полую группу образуют события D и F.
События, образующие полную группу, называются единственно возможными. Например, при наблюдении в течение некоторого времени за эксплуатацией устройства релейной защиты (РЗ) ЛЭП полная группа включает следующие события:
А1 - устройство работало безотказно;
А2. - наблюдался отказ устройства (РЗ не отключила ЛЭП при недопустимом режиме);
А3 – наблюдалось ложное срабатывание устройства (РЗ отключила ЛЭП при отсутствии необходимости к срабатыванию).
 Противоположными называют такие два события, для которых появление одного заключается в непоявлении другого. Если событие обозначено как А, то противоположное событие обозначается
Противоположными называют такие два события, для которых появление одного заключается в непоявлении другого. Если событие обозначено как А, то противоположное событие обозначается 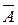 («не А»).
(«не А»).
Примером противоположных событий являются состояния работоспособности R и отказа (неработоспособности) 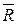 объекта. Если работоспособное состояние системы на диаграмме Венна (рис. 5).представлено в виде некоторой замкнутой области R, то вся остальная часть квадрата соответствует отказу системы – событие
объекта. Если работоспособное состояние системы на диаграмме Венна (рис. 5).представлено в виде некоторой замкнутой области R, то вся остальная часть квадрата соответствует отказу системы – событие 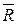 .
.
П ротивоположные события всегда образуют полную группу.
Чтобы не ошибиться в определении противоположного события достаточно внимательно отнестись к расположению частицы НЕ в описании этого события. Так, если событие П – получение оценки пять на экзамене, то событием 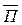 является получение оценки не пять, т.е. два, три или четыре.
является получение оценки не пять, т.е. два, три или четыре.
Аналогично действиям над числам и функциям в алгебре, события можно умножать, складывать и вычитать. Действиями над событиями занимается раздел математики называемый «алгебра событий» Основными понятиями алгебры событий являются произведение, сумма и разность событий.
 Произведением (пересечением) событий А и В называется такое событие С, которое заключается в появлении и события А исобытия В совместно (рис.6): АВ = С.
Произведением (пересечением) событий А и В называется такое событие С, которое заключается в появлении и события А исобытия В совместно (рис.6): АВ = С.
Понятие «произведение» может применяться к любому количеству событий.
Наличие во фразе, описывающей событие, союза И является признаком произведения событий.
 Например,для двухтрансформаторной ТП (рис.7) возможны события:
Например,для двухтрансформаторной ТП (рис.7) возможны события:
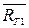 – отказ первого трансформатора;
– отказ первого трансформатора;
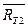 – отказ второго трансформатора.
– отказ второго трансформатора.
Тогда 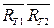 – отказ и того и другого трансформатора совместно.
– отказ и того и другого трансформатора совместно.
Суммой (объединением) событий А+В называется такое событие С, которое заключается в появлении или события А, или события В, или того и другого совместно (рис. 8): А+В = С.
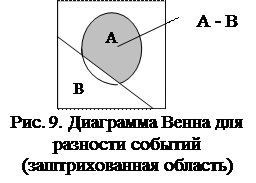
 Наличие союза ИЛИ является признаком суммы событий.
Наличие союза ИЛИ является признаком суммы событий.
Понятие «сумма» может применяться к любому количеству событий.
Важно подчеркнуть, что для совместных событий (рис. 8-а) их сумма включает в себя и их произведение.
Например, для двухтрансформаторной подстанции (рис. 7) сумма 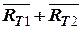 заключается в отказе 1-го или 2-го трансформаторов или двух трансформаторов совместно.
заключается в отказе 1-го или 2-го трансформаторов или двух трансформаторов совместно.
Разностью событий А-В называется такое событие С, которое заключается в появлении события А при обязательном непоявлении события В (рис. 9): А – В = С.
Например, для двухтрансформаторной подстанции (рис. 7) разность 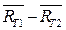 заключается в отказе 1-го трансформатора при работоспособности 2-го.
заключается в отказе 1-го трансформатора при работоспособности 2-го.
Использование понятий алгебры событий позволяет описывать сложные события в максимально сокращённом виде.
Пример 3
Для нижеприведенной схемы электроснабжения (рис. 10) записать события, заключающиеся в работоспособности RC и отказе 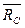 системы, обозначая состояния работоспособности и отказа элементов буквами Ri и
системы, обозначая состояния работоспособности и отказа элементов буквами Ri и 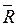 i соответственно.
i соответственно.
 Решение. Для описания состояния системы сначала составляется полная фраза, описывающая это состояние (обычно достаточно сделать это устно): работоспособность системы Rс заключается в работоспособности всех её элементов. Сформулирована эта фраза должна быть так, чтобы в ней присутствовали ключевые слова – союзы И и ИЛИ: Система работоспособна, когда работоспособен «И» генератор RГ, «И» первый трансформатор RТ1, «И» линия RЛ, «И» второй трансформатор RТ2. Так как союз «и» является признаком произведения событий, записываем: Rс = RГ RТ1 RЛ RТ2.
Решение. Для описания состояния системы сначала составляется полная фраза, описывающая это состояние (обычно достаточно сделать это устно): работоспособность системы Rс заключается в работоспособности всех её элементов. Сформулирована эта фраза должна быть так, чтобы в ней присутствовали ключевые слова – союзы И и ИЛИ: Система работоспособна, когда работоспособен «И» генератор RГ, «И» первый трансформатор RТ1, «И» линия RЛ, «И» второй трансформатор RТ2. Так как союз «и» является признаком произведения событий, записываем: Rс = RГ RТ1 RЛ RТ2.
Система неработоспособна 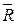 С, если отказал генератор
С, если отказал генератор 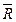 Г, «ИЛИ» отказал первый трансформатор
Г, «ИЛИ» отказал первый трансформатор 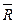 Т1, «ИЛИ» отказала линия
Т1, «ИЛИ» отказала линия 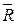 Л, «ИЛИ» отказал второй трансформатор
Л, «ИЛИ» отказал второй трансформатор 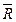 Т2, «ИЛИ» произошел отказ любой пары элементов схемы, ИЛИ любой тройки, «ИЛИ» отказали все четыре элемента. Так как союз «или» является признаком суммы событий, записываем:
Т2, «ИЛИ» произошел отказ любой пары элементов схемы, ИЛИ любой тройки, «ИЛИ» отказали все четыре элемента. Так как союз «или» является признаком суммы событий, записываем: 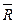 С =
С = 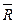 Г +
Г + 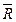 Т1 +
Т1 +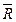 Л +
Л + 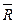 Т2.
Т2.
Следует обратить внимание, что добавлять в окончательное выражение для 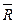 С произведения отказов, взятые парами, тройками или четверкой не нужно, так как это приведёт к тавтологии – понятие суммы для четырёх событий уже включает в себя появление событий, взятых по одному, по два, по три или сразу всех вместе.
С произведения отказов, взятые парами, тройками или четверкой не нужно, так как это приведёт к тавтологии – понятие суммы для четырёх событий уже включает в себя появление событий, взятых по одному, по два, по три или сразу всех вместе.
 Пример 4
Пример 4
Для схемы включения электрических ламп (рис. 11) записать выражения: «в цепи протекает ток» - Rс, «ток в цепи не протекает» - 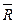 С, обозначая состояния работоспособности и отказа ламп буквами RЛi и
С, обозначая состояния работоспособности и отказа ламп буквами RЛi и 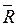 Лi соответственно.
Лi соответственно.
Решение. Ток в цепи будет протекать (т. е. система будет работоспособна - Rс), когда будут работоспособны первая R1 «И» четвертая R4 лампы «И» хотя бы одна (любая) из двух оставшихся, т.е. «ИЛИ» вторая R2, «ИЛИ» третья R3, «ИЛИ» вторая «И» третья совместно: RС = R1R4(R2 + R3).
Тока в цепи не будет 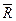 С, если откажет «ИЛИ» первая лампа
С, если откажет «ИЛИ» первая лампа 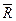 1, «ИЛИ» четвертая
1, «ИЛИ» четвертая 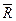 4, «ИЛИ» вторая
4, «ИЛИ» вторая 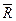 2 «И» третья
2 «И» третья 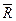 3 совместно, «ИЛИ» откажут совместно любые три «ИЛИ» все четыре лампы:
3 совместно, «ИЛИ» откажут совместно любые три «ИЛИ» все четыре лампы: 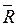 C =
C = 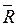 1 +
1 + 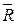 4 +
4 + 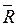 2
2 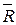 3.
3.
Из рассмотренных примеров видно, что для безошибочного решения подобных задач необходимо сначала устно с использованием союзов И, ИЛИ сформулировать интересующее событие, а затем кратко записать его с использованием понятий алгебры событий и выбранных обозначений.
Логические схемы анализа надежности
Пример 5
Система состоит из трех независимо работающих элементов. Записать выражения для состояний RС и 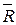 С, если известно, что она отказывает при отказе любого элемента (примером такой системы является автомобиль, который можно считать состоящим из трёх независимо работающих элементов – двигателя, ходовой части и водителя, – отказ любого из них приводит к отказу системы).
С, если известно, что она отказывает при отказе любого элемента (примером такой системы является автомобиль, который можно считать состоящим из трёх независимо работающих элементов – двигателя, ходовой части и водителя, – отказ любого из них приводит к отказу системы).
Решение. Следуя рассуждениям, приведённым в примерах 3 и 4 можно записать:
Rс = R1 R2 R3; 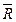 с =
с = 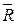 1 +
1 + 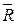 2 +
2 + 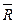 3.
3.
Сравнение этих выражений с выражениями, записанными в примере №3, показывает их полную идентичность. Это свидетельствует о том, что систему, о которой идёт речь в рассматриваемой задаче, можно представить в виде простейшей электрической цепи из трёх последовательно соединённых элементов, иначе говоря, в виде логической схемы анализа надёжности.
Логической схемой анализа надёжности называется схема, в которой реальные объекты и составляющие их элементы с целью облегчения анализа надежности представляются в виде простейшей электрической цепи. На логических схемах реальные элементы заменяются сопротивлениями, включенными в электрическую цепь. Логическая схема отображает не фактические взаимосвязи элементов (механические, электрические и пр.), а только их функциональные взаимосвязи, то есть показывает, как состояние отдельных элементов системы влияет на состояние системы в целом.
Анализ надёжности при использовании логической схемы сводится к решению вопроса, при каких состояниях элементов в цепи будет (или, наоборот, не будет) протекать ток.
Элементы на логической схеме соединяются
· последовательно, если отказ любого из них приводит к отказу системы;
· параллельно, если система отказывает при отказе всех элементов.
 Пример 6
Пример 6
Имеется батарея из трех параллельно соединенных конденсаторов (рис. 12). Изобразить логическую схему анализа надёжности, описывающую такую систему.
Решение. В рассматриваемой задаче элементы электрически соединены между собой параллельно. Поэтому естественным будет предположение, что логическая схема тоже должна быть параллельной (рис.13). Однако такое представление системы будет неполным.
 Параллельное соединение элементов логической схемы предполагает, что система сохраняет работоспособность при сохранении работоспособности хотя бы одного из её элементов. Это будет выполняться при обрыве цепей отдельных конденсаторов (если пренебречь тем, что такой обрыв меняет общую ёмкость батареи, что в некоторых случаях может приводить к отказу системы в целом, так как одна из важнейших её характеристик – ёмкость - выходит за установленные пределы).
Параллельное соединение элементов логической схемы предполагает, что система сохраняет работоспособность при сохранении работоспособности хотя бы одного из её элементов. Это будет выполняться при обрыве цепей отдельных конденсаторов (если пренебречь тем, что такой обрыв меняет общую ёмкость батареи, что в некоторых случаях может приводить к отказу системы в целом, так как одна из важнейших её характеристик – ёмкость - выходит за установленные пределы).
Необходимо учесть, что обрыв является не единственной причиной отказа конденсатора. 2-я причина отказа – короткое замыкание (КЗ) между обкладками. При таком отказе даже в одном конденсаторе из строя выходит вся батарея. С позиции КЗ батарея на логической схеме представляет собой три сопротивления, включенные последовательно.
Таким образом, в целом на логической схеме (рис. 14) батарея конденсаторов должна быть представлена шестью элементами – три, характеризующие отказы «типа обрыв», три – отказы «типа КЗ».
 Данный пример наглядно показывает, какие действия необходимо предпринять при составлении логической схемы анализа надежности:
Данный пример наглядно показывает, какие действия необходимо предпринять при составлении логической схемы анализа надежности:
1) Выяснить, в чём заключается отказ и работоспособность системы.
2) Выяснить, какие типы отказов могут наблюдаться у отдельных элементов системы (например, отказ «типа обрыв», отказ «типа короткое замыкание»).
3) Выяснить, как различные типы отказов влияют на работоспособность системы.
4). Изобразить логическую схему, учитывающую функциональные связи элементов и системы.
Когда на логической схеме элементы изображены соединенными параллельно, можно говорить о том, что в этой системе используется резервирование.
Резервирование – это метод повышения надежности путем введения избыточности.
Избыточность – это дополнительные средства и возможности сверх минимально необходимых для выполнения объектом поставленной задачи.
Под основными понимаются элементы, минимально необходимые для выполнения задачи; под резервными – элементы, используемые сверх основных.
Например, в двухтрансформаторной ТП (рис. 7) один трансформатор основной, второй – резервный; в автомобиле 4 колеса основные, 5-е (запасное) – резервное.
Существуют различные типы резервирования:
- структурное - введение избыточных структурных элементов, например, трансформаторов, ЛЭП, электродвигателей;
- временное - использование избыточного времени (запаса времени) для выполнения поставленной задачи;
- нагрузочное – использование избыточности по нагрузке, например, трансформатор, рассчитанный на некоторую мощность, реально загружен на 70% этой мощности.
Вероятность события. Формулы непосредственного расчета вероятности
Термином «вероятно» достаточно часто пользуются в обыденной жизни: «вероятно, будет дождь», «вероятно, я сдам экзамен успешно». Говоря так, мы интуитивно вкладываем в этот термин разную степень нашей уверенности в возможности появления события. Но, конечно, не о каких численных оценках этой возможности речь не идёт.
Математиками такая количественная оценка предложена.
Вероятность события – это количественная мера возможности появления события в опыте.
Ввиду того, что вероятность является искусственно придуманной характеристикой, было целесообразным сделать её удобной к применению, позволяющей без труда оценивать степень приближения события к достоверному или невозможному. Такой, удобной для анализа, характеристика будет в случае, когда меняется в пределах от нуля до единицы.
Принято, что невозможные события имеют вероятность, равную нулю, а достоверные – единице, вероятность между нулём и единицей имеют случайные события.
Чаще всего для обозначение вероятности используется латинская буква Р (по-французски вероятность – probabilite´). Обозначается вероятность события А, как Р(А) или ра.
 2014-02-24
2014-02-24 1480
1480