Теплопроводность цилиндрической стенки

Пусть заданы ГУ I рода, т. е. 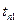и 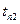= const, требуется найти t(r) и q, (рис.1.9).

Положим , , , .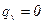

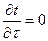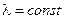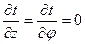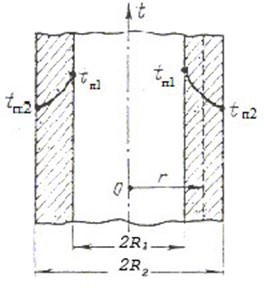
Рис.1.9. Теплопроводность цилиндрической стенки

Здесь нужно брать дифференциальное уравнение теплопроводности в цилиндрической системе координат (см. уравнение (1.10) при факторе геометрической формы k=2 для цилиндра).

Математическая постановка задачи имеет вид

Дифференциальное уравнение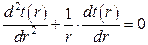

Граничные условия: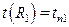

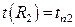
Уравнение теплопроводности решаем путем введения подстановки: u=dt/dr.

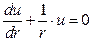. Разделяем переменные и интегрируем 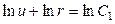. После потенцирования получим .

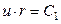Вспоминаем, что u=dt/dr, разделяем переменные .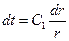

Интегрируем и получаем общее решение 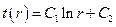. (1.31)

После определения С₁ и С₂ с помощью граничных условий, получим

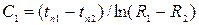и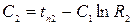

Окончательно 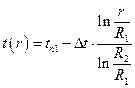. (1.26)

Здесь температура вдоль стенки изменяется по логарифмическому закону.

Удельный тепловой поток найдем с помощью закона Фурье:

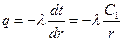, где 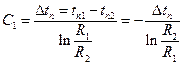, (1.28)

Здесь, в отличие от плоской стенки, тепловой поток зависит от радиуса ,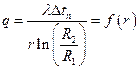

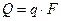, где боковая поверхность цилиндра .

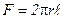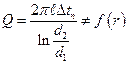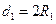Тогда , где и .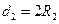

Опять неудобно, нужно сделать чтобы было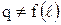. Введем понятие линейной плотности теплового потока

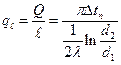, Вт/м. (1.27)

В знаменателе стоит термическое сопротивление цилиндрической стенки, мК/Вт.

Термические напряжения в цилиндрической стенке определяются по уравнениям (1.11) и (1.12) в которых использование формулы (1.13) для нахождения средней температуры может привести к значительным погрешностям. Более точно среднемассовая температура полого цилиндра внутренним радиусом 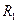и наружным 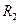может быть найдена по следующей формуле:

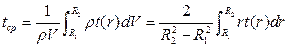, (1.28)

где 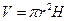- объем цилиндра радиусом r и высотой H; ;

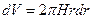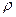- плотность материала стенки, 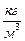; произведение 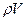- масса, кг.

Подставляя в уравнение (1.28) решение (1.31) для поля температур в виде 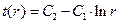и производя интегрирование, получим для средней по массе температуре цилиндрической стенки

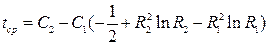. (1.29)

При малых перепадах температур 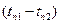для приближенных расчетов при определении 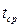можно использовать уравнение (1.13).