10. Если функции, имеющие предел в некоторой точке совпадают на множестве сгущающемся в этой точке, то их пределы равны.
20. Если последовательности, имеющие предел, содержат совпадающие подпоследовательности, то их пределы равны.
30. Если функции совпадают в проколотой окрестности предельной точки, то их пределы равны в случае существования.
40. Если две последовательности совпадают, начиная с некоторого номера, то их пределы существуют или не существуют одновременно, и в случае существования равны.
50. Если из двух функций одна не превышает другой в проколотой окрестности предельной точки, то предел первой не превосходит предела второй в случае их существования.
60. Если предел одной функции больше предела второй в некоторой точке, то существует проколотая окрестность этой точки, в которой первая функция больше второй.
∆ 10,20: 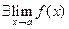 ,
, 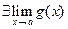 и имеется множество
и имеется множество 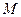 :
:
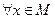
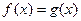
 .
.
Тогда 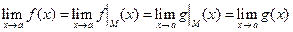 .
.
30,40: Во-первых: 
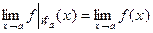 .
.
Во-вторых: 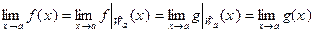 .
.
60: Пусть 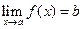 ;
; 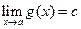 ;
; 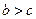 , тогда
, тогда
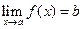
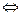
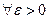
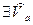
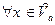
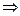
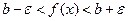 ,
,
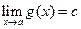
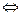
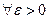
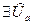
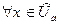
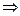
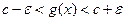 .
.
Выберем 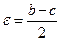 ;
; 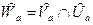 ,
,
тогда 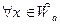
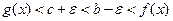 .
.
50: Пусть 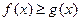
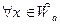 .
.
Докажем, что 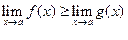 .
.
Доказательство здесь проведем от противного.
Допустив, что 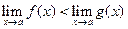 , получим по п.60
, получим по п.60 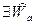
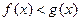 ,
,
а это противоречит условию теоремы. ▲
и, наконец
Т0. (Принцип двустороннего ограничения, теорема о двух милиционерах).
Если две функции имеют общий предел и в окрестности предельной точки третья функция заключена между ними, то она имеет тот же предел.
∆ следует из 50 и 60.
Пусть 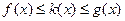
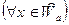 ,
,
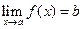
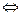
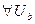
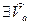
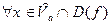
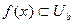 ,
,
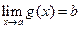
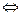
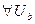
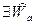
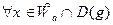
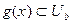
и, т.к. 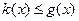 и
и 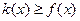 ,
,
то 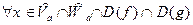
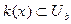
т.е. 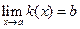 . ▲
. ▲
 2014-02-24
2014-02-24 2733
2733








