2014-02-24
1796
Мы уже установили, что последовательность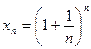 
монотонно возрастает, ограничена сверху и 
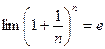, а последовательность 
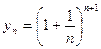монотонно убывает, ограничена снизу и 
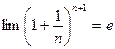. Тогда:
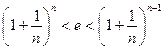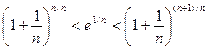Þ 
Þ
Þ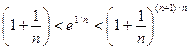 
.
Логарифмируем неравенство: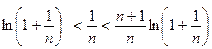 
. Получаем два неравенства:
а)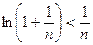
; б)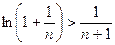
.
Следовательно: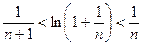 
.
Заменив в этом неравенстве n на – n получим:
.
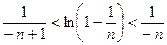Объединяем полученные выше два неравенства:
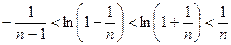. Выбирая 
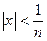, получаем: 
.
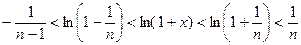Т.е.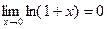 
или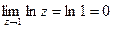 
.
Следовательно, функция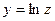 
непрерывна в точке 
.
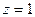Теперь рассмотрим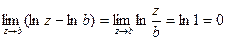 
.
Отсюда заключаем, что: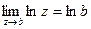 
.
Следовательно, функция 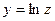непрерывна в точке 
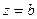" b Î R.
