Рассмотрим систему функций 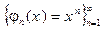 . Если взять эту систему функций в качестве шкалы асимптотического сравнения при
. Если взять эту систему функций в качестве шкалы асимптотического сравнения при 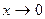 , то справедливы следующие асимптотические разложения:
, то справедливы следующие асимптотические разложения:
1˚. 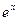 ≃
≃ 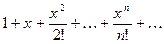
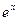 ≃
≃ 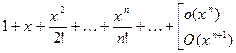
2˚. 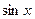 ≃
≃ 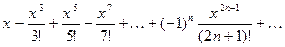
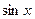 ≃
≃ 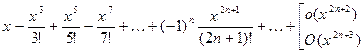
3˚. 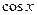 ≃
≃ 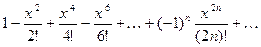
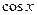 ≃
≃ 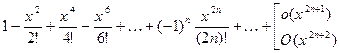
4˚. 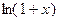 ≃
≃ 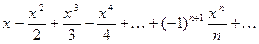
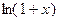 ≃
≃ 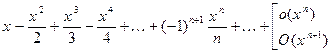
5˚. 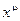 ≃
≃ 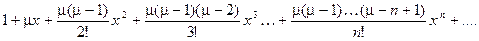
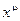 ≃
≃ 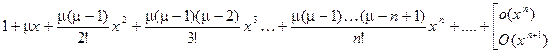
§ Теорема о вложенных промежутках (Коши-Кантора)
Т˚. Во всякой последовательности вложенных друг в друга замкнутых промежутков, длины которых стремятся к нулю, содержится единственная точка, принадлежащая всем промежуткам одновременно: 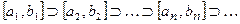
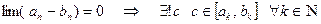 .
.
Δ Последовательность: 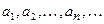 - возрастающая и ограниченная сверху (любым
- возрастающая и ограниченная сверху (любым 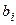 ), следовательно по теореме Вейерштрасса имеет предел:
), следовательно по теореме Вейерштрасса имеет предел: 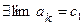 .
.
Последовательность 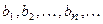 - убывающая и ограниченная снизу (например, одним из
- убывающая и ограниченная снизу (например, одним из 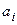 ), т.е.
), т.е. 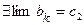 .
.
Тогда: 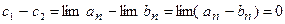 , т.е.
, т.е. 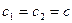 ▲
▲
 2014-02-24
2014-02-24 1869
1869







