Теорема о предельной точке

Теорема (Бореля-Лебега) о конечном покрытии.

Def. Система множеств 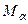, где α пробегает некоторое множество А называется покрытием множества Х, если .

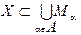Def. Если все 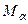- открытые множества, то покрытие называется открытым, если множество А – конечно, то покрытие называется конечным.

Def. Всякая подсистема множеств покрытия, которая тоже покрывает данное множество называется подпокрытием покрытия .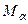

Т˚. Всякое покрытие замкнутого промежутка интервалами содержит конечное подпокрытие. (Из всякого покрытия замкнутого промежутка интервалами можно выделить конечное).

Δ Доказательство теоремы проведем от противного.

Пусть из некоторого покрытия [ a, b ] нельзя извлечь [—————|—————]

конечное. Разделим отрезок пополам точкой c a b c

Тогда, по крайней мере, для одного из промежутков [ a,c ] или [ c,b ] нет конечного подпокрытия. Обозначим этот промежуток 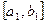. Aналогично, (продолжая процедуру), получим: 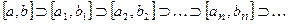и 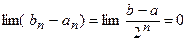. Т.е. существует только одна общая точка всех интервалов. Для точки с существует интервал I из покрытия, такой что с Î I - и этот интервал покрывает 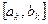начиная с некоторого k. Это противоречит тому, что ни один из этих промежутков не имеет конечного покрытия.

Предположение о том, что из бесконечного открытого покрытия замкнутого промежутка нельзя выделить конечное подпокрытие привело к противоречию. Это доказывает теорему.▲

Т˚. (Больцано-Вейерштрасса). Всякая ограниченная бесконечная последовательность содержит сходящуюся подпоследовательность.

На расширенной вещественной прямой:

Всякая бесконечная последовательность содержит подпоследовательность, имеющую предел, возможно несобственный. Δ▲.

Следствие˚. Всякое ограниченное бесконечное множество имеет хотя бы одну предельную точку. На расширенной числовой прямой всякое бесконечное множество имеет хотя бы одну предельную точку, возможно несобственную.