Дифференцируемой на промежутке

Необходимое и достаточное условие постоянства функции,

РАЗДЕЛ. Изучение свойств функций с помощью производных

Т°. Функция f (x) непрерывная на [ a, b ] и дифференцируемая на (a, b) постоянна тогда и только тогда когда ее производная равна нулю.

D 1) f (x) = const Þ .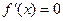

2) 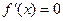Þ 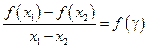, 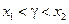(по теореме Лагранжа) Þ

f (x ₁) – f (x ₂) = (x ₁ – x ₂) f (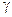) = 0 Þ f (x ₁) = f (x ₂). ▲