Т°. Если в окрестности точки внутреннего экстремума 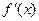 меняет знак с “ – ” на ” + ” то в критической точке имеется минимум функции; если
меняет знак с “ – ” на ” + ” то в критической точке имеется минимум функции; если 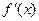 меняет значение с “ + ” на ” – ” то в точке х 0 функция имеет максимум.
меняет значение с “ + ” на ” – ” то в точке х 0 функция имеет максимум.

Т°. Пусть в т. х 0 функция 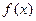 n – кратно дифференцируема, причем все производные
n – кратно дифференцируема, причем все производные
f (k)(x 0) до (n – 1) включительно равны нулю, и f ( n )(x 0) ¹ 0 то в точке х = х 0:
при четном n функция имеет минимум если 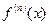 > 0 и максимум если
> 0 и максимум если 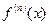 < 0;
< 0;
при нечетном n функция не имеет экстремума. Она возрастает если 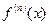 > 0 и убывает если
> 0 и убывает если 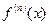 < 0.
< 0.
D Утверждения следуют из разложения функции f (x) в ряд Тейлора в точке х 0:
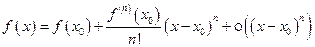 . ▲
. ▲
Задачи для исследования функций на экстремумы:
Для нижеуказанных функций установить характер экстремума в точке х = 0:
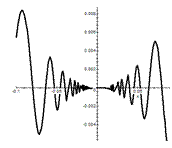 1).
1). 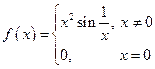 ; 2).
; 2). 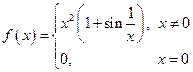 ;
;
3). 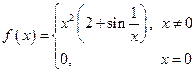 ; 4).
; 4). 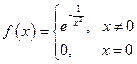 .
.
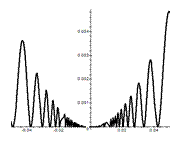
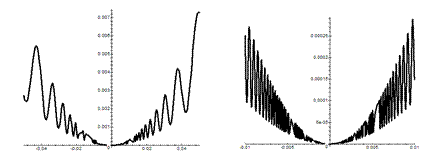
На иллюстрациях приведены эскизы первых трех функций. Вверху справа – для функции 1, внизу справа – для функции 2, внизу – две иллюстрации к функции 3, но в разных масштабах. Слева для 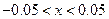 , справа для
, справа для 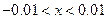 . Они показывают динамику изменения функции при
. Они показывают динамику изменения функции при 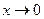 . Для функции 4 исследование следует провести самостоятельно.
. Для функции 4 исследование следует провести самостоятельно.
 2014-02-24
2014-02-24 422
422








