Пример вычисления предела с помощью формулы Тейлора

При вычислении предела воспользуемся разложением числителя и знаменателя в ряд Тейлора:

.

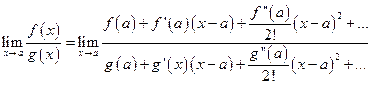Проанализируем записанную формулу.

*. Если 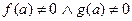, то предел равен .

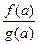*. Если 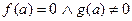, то предел равен нулю.

*. Если 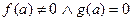, то предел равен бесконечности.

*. Если 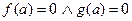, то, сокращая числитель и знаменатель дроби на 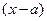, выясняем, что:

**. Если 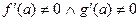, то предел равен 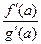, что равносильно применению

правила Лопиталя.

**. Если 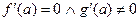, то предел равен нулю.

**. Если 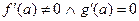, то предел равен бесконечности.

**. Если 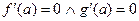, то, сокращая числитель и знаменатель дроби еще раз на 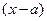, выясняем, что:

***. Если 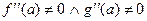, то предел равен 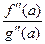, что равносильно повторному применению правила Лопиталя.

***. Если 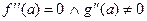, то предел равен нулю.

***. Если 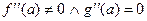, то предел равен бесконечности.

***. Если 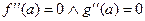, то, …. ….. …..

Таким образом ясно, что применение правила Лопиталя и использование разложения функций в ряды Тейлора по сути одно и тоже (с естественными оговорками по поводу дифференцируемости).

Практический совет: Если функции, стоящие в числителе и знаменателе дроби имеют известные разложения в ряды Тейлора или эти разложения могут быть легко получены, то следует этим воспользоваться. Если же получение вышеупомянутых разложений связано со значительными техническими трудностями, то более рациональным является применение правила Лопиталя.