2014-02-24
8557
А. Дробно-линейные иррациональности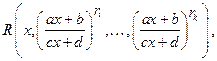 
.
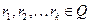Записав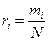 
(N -общий знаменатель дробей 
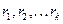), получим:
= 
.
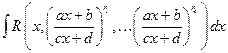
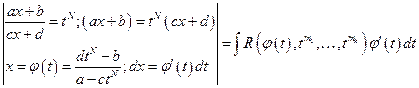Получен интеграл от рациональной функции.
Примеры: 1°.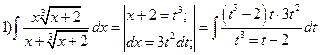 
.
2°.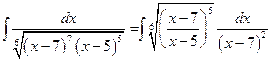 
=
= 
= 
.
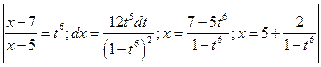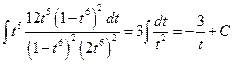Возвращаясь к исходной переменной, получим:
= 
.
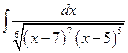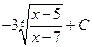Б. Интегрирование дифференциального бинома (биномиального дифференциала):
.
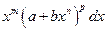Теорема Чебышева: Если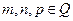 
,то интеграл от дифференциального бинома выражается через элементарные функции тогда и только тогда когда:
1°.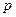 
– целое; 2°. 
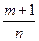– целое; 3°. 
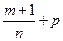– целое.
и при этом следующие подстановки (Чебышева) сводят интегралы к интегралам от рациональных функций.
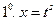,где s – общий знаменатель дробей m и n,
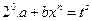, s – знаменатель дроби p,
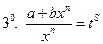, s – знаменатель дроби p.
Примеры:
1°.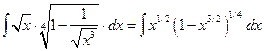 
= 
=
= 
=
= 
.
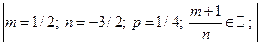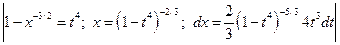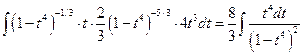С помощью второй подстановки Чебышева интеграл от дифференциального бинома стал интегралом от рациональной функции.
2°.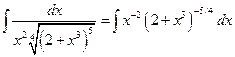 
= 
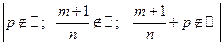. Ни одна из подстановок Чебышева не подходит – интеграл не может быть выражен через элементарные функции (не берётся).
3°.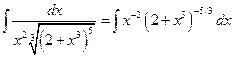 
=…
В данном случае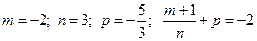 
и, следовательно, третья подстановка Чебышева должна рационализовать подынтегральное выражение.
В самом деле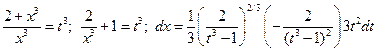 
, и получается интеграл
… = 
= 
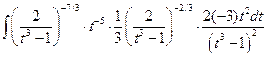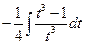, и интеграл рационализован.
4°.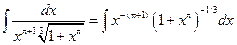 
=…
Здесь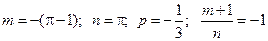 
и выполняя замену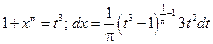 
, получим
… = 
.
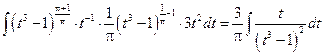Приведенный пример показывает что для не рациональных показателей степеней подстановки Чебышева тоже могут быть полезны.
В. Подстановки Эйлера: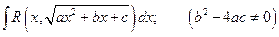 
;
Для интегрирования квадратичных иррациональностей
I.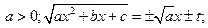 
II.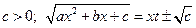 
;
III.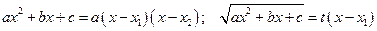 
.
Других случаев просто нет, ибо тогда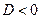 
. Знаки плюс–минус выбираются из соображений удобства. Остроумие подстановок Эйлера заключается в том, что для нахождения х получается линейное уравнение.
1°.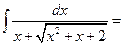 
… Учитывая что 
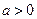, выполним первую подстановку Эйлера.
… = 
= 
= 
.
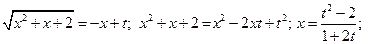
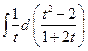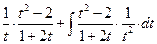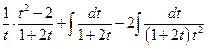Полученные интегралы от рациональных функций трудностей не представляют.
2°.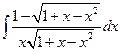 
= … Учитывая что 
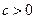, выполним вторую подстановку Эйлера.
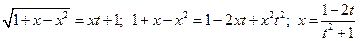. Тогда … = 
.
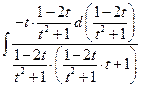Вновь получен интеграл от рациональной функции.
3°.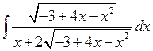 
= … Квадратный трехчлен под знаком корня имеет вещественные корни 
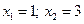поэтому можно применить третью подстановку Эйлера.
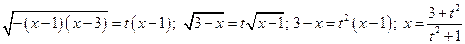и получаем
= 
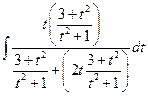, а это интеграл от рациональной функции.
Г°. Интегрирование иррациональностей вида: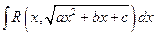 
.
Введем обозначение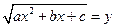 
.
Г1°.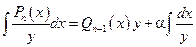 
.
Для нахождения коэффициентов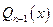 
и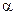 
продифференцируем обе части равенства:
в левой части перейдем к к общему знаменателю: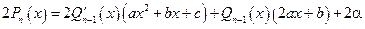 
. Многочлены стоящие в числителях дробей справа и слева от знака равенства должны быть равны и, следовательно, должны быть равны коэффициенты при соответствующих степенях переменной. Отсюда получаем систему линейных уравнений для нахождения коэффициентов 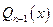и .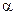
Пример: 1°.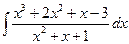 
= …
Г2°.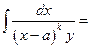 
…
Замена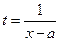 
; 
; 
;
= 
= 
=
= 
= 
.
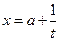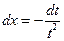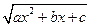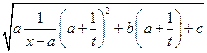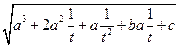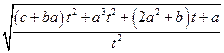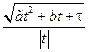После замены переменной, получим
… = 
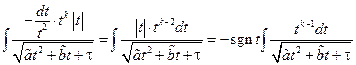– а такой интеграл рассмотрен в предыдущем пункте.
Пример: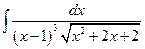 
= ….
Г3°.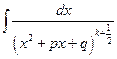 
= …
Подстановка Абеля: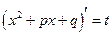 
; 
; 
= 
(*).
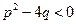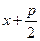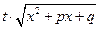Находя дифференциал от правой и левой части равенства (*), получим:
; 
; 
;
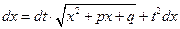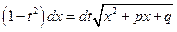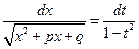а возводя правую и левую части равенства (*) в квадрат, будем иметь:
; 
.
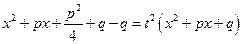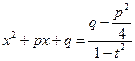Т.е. после выполнения подстановки Абеля, исходный интеграл станет интегралом от рациональной функции:
… = 
.
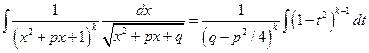Г4°.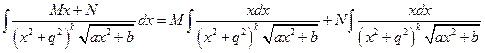 
.
В первом интеграле делаем замену: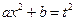 
, а во втором 
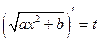и задача интегрирования интеграла типа Г4° сведена к интегрированию рациональных функций.
Г5°.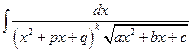 
= ….
Возможны варианты:
а)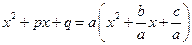 
и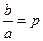 
; 
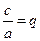тогда получим интеграл, рассмотренный в пункте Г3°, и применим подстановку Абеля.
б)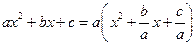 
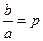и тогда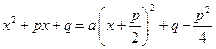 
; 
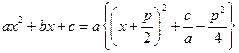и после замены 
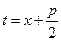у квадратных трехчленов не останется первых степеней (интегралы типа Г4°).
в) В случае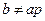 
сделаем дробно-линейную подстановку 
, (
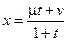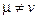). Тогда 
= 
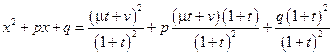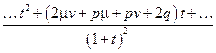и потребуем, чтобы коэффициент при первой степени t равнялся нулю:
.
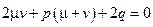Аналогично, для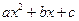 
:
.
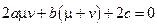Из двух полученных уравнений находим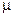 
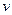
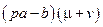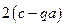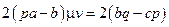и 
= 
; 
и,
следовательно: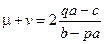 
; 
.
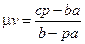Таким образом 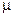и 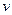есть корни квадратного уравнения: 
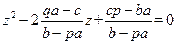. После замены 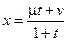в квадратных трехчленах не остается первых степеней (интегралы типа Г4°).
