Элементарные функции (не берущиеся интегралы )

Интегралы, которые не могут быть выражены, через

1°. Интегральная экспонент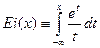а: ;

Тогда , .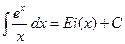

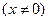При этом 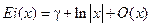, если,

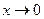Где 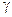– постоянная Эйлера и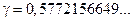

Рекуррентная формула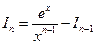

позволяет вычислять интегралы вида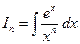

2°. Интегральный логагифм: ;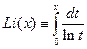

Тогда .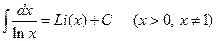

Кроме того ,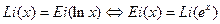

.

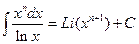3°. Интеграл Коши – функция ошибок: ;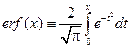

Тогда 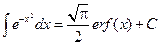. Название и обозначение от – error function – функция ошибок. Функция нечетная: .

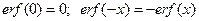Функция 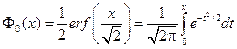называется интегралом вероятностей (Эйлера- Пуассона).

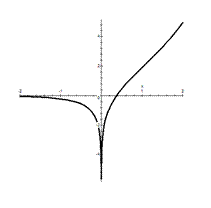
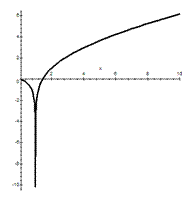
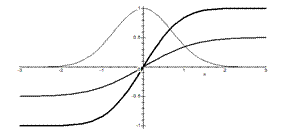
На рисунке изображены: функция 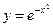– «колокольчик», изображенный самой тонкой линией; функция 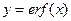– изображена самой толстой линией. Ее амплитуда в два раза больше амплитуды интеграла вероятностей, также изображенного на рисунке, но средней по толщине линией.