Примеры.
1°. 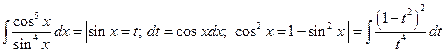 .
.
2°. 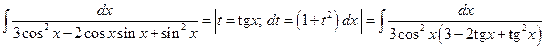 =
=
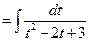 .
.
3°. 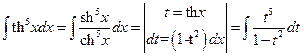 = ….
= ….
4°. 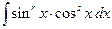 = …
= … 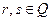 .
.
Замена 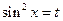 ;
; 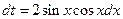 .
.
…= 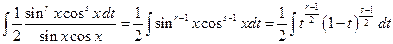 – (интеграл от дифференциального бинома).
– (интеграл от дифференциального бинома).
В°. Очень полезными являются две следующие формулы:
1°. 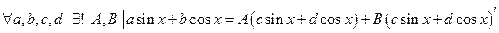 и, следовательно, интегрируя получаем:
и, следовательно, интегрируя получаем:
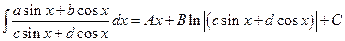 .
.
Пример. 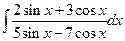 = ….
= ….
2°. 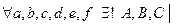
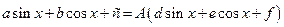 +
+ 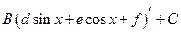
и интегрируя, получаем:
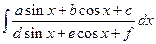 =
= 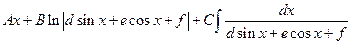 ;
;
при взятии последнего интеграла полезно знать, что: 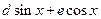 =
= 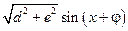 .
.

Рассматриваются интегралы вида:
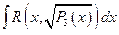 и
и 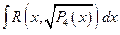 , (*)
, (*)
где 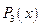 и
и 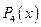 – многочлены 3й и 4й степени соответственно, с вещественными коэффициентами и не имеющие кратных корней. В случае кратных корней радикалы упрощаются и сводятся к ранее рассмотренным иррациональностям.
– многочлены 3й и 4й степени соответственно, с вещественными коэффициентами и не имеющие кратных корней. В случае кратных корней радикалы упрощаются и сводятся к ранее рассмотренным иррациональностям.
Эти интегралы, как правило, не интегрируются в элементарных функциях и называются эллиптическими .
Однако:
1°. 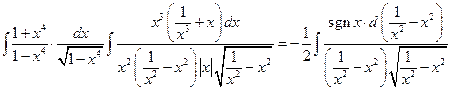 =
= 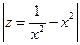 =
=
= 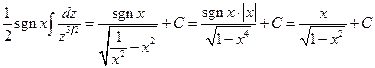 .
.
2°. Легко видеть, что: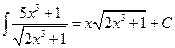 .
.
Два рассмотренных интеграла, хотя и являются интегралами вида (*) выражаются через элементарные функции. Такие интегралы называются псевдоэллиптическими .
А°. Для 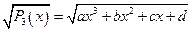 :
:
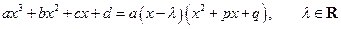
Сделаем замену: 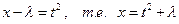
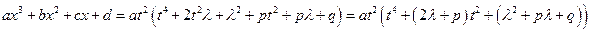
следовательно:
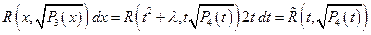
Б°. Для интегрирования 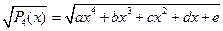 запишем
запишем
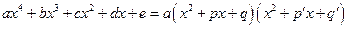 .
.
В получившихся квадратных трехчленах избавимся от членов содержащих первые степени переменной х.
а) При 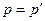 сделаем замену
сделаем замену 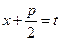 Þ
Þ 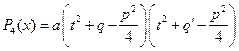 .
.
б) При 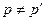 сделаем замену
сделаем замену 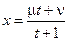 .
.
Тогда 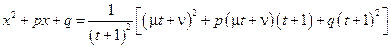 ,
,
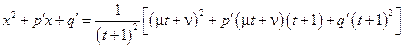 .
.
Неизвестные параметры 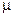 и
и 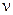 найдем из условия равенства нулю коэффициентов при первых степенях переменной
найдем из условия равенства нулю коэффициентов при первых степенях переменной 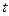 :
:
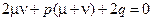 и
и 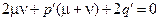 .
.
Из системы уравнений: 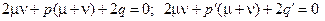 находим
находим 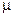 и
и 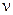 .
.
Тогда: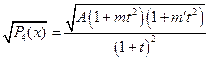 и
и 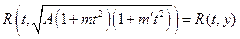 .
.
Теперь представим: 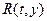 в виде
в виде 
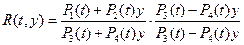 =
=
= 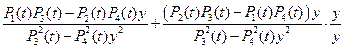 =
= 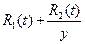 .
.
Интеграл от первого слагаемого легко берется
В°. Рассмотрим интеграл: 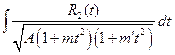 . (**)
. (**)
Функцию 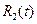 запишем в виде
запишем в виде 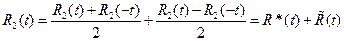 .
.
Запишем
Функция 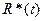 четная и, следовательно
четная и, следовательно 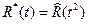 ,
,
а функция 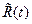 нечетная и поэтому
нечетная и поэтому 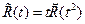 .
.
Тогда интеграл (**) разбивается в сумму двух интегралов:
I. 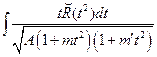 . Замена
. Замена 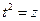 сводит этот интеграл, к ранее рассмотренным интегралам от квадратичных иррациональностей.
сводит этот интеграл, к ранее рассмотренным интегралам от квадратичных иррациональностей.
II. 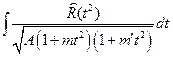 . Этим интегралом мы и займемся в следующем параграфе. §. Приведение интеграла
. Этим интегралом мы и займемся в следующем параграфе. §. Приведение интеграла 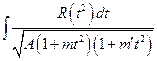 к каноническому виду.
к каноническому виду.
Приведение интеграла к каноническому виду зависит от знаков констант А, m, 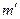 .
.
Есть шесть различных вариантов распределения знаков этих констант:
1) + – –; 2) + – +; 3) + + +; 4) – – –; 5) – – +; 6) – + +.
Введем обозначения: 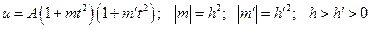
и рассмотрим каждый из шести выделенных случаев.
1°. 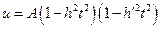 . Область определения подынтегрального выражения
. Область определения подынтегрального выражения
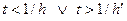 .
.
a) 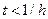 ; Производя замену переменной интегрирования
; Производя замену переменной интегрирования 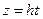 получаем:
получаем:
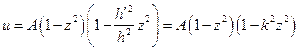 и
и 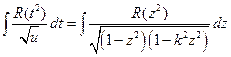 .
.
Здесь 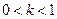 . Последний интеграл записан уже в каноническом виде.
. Последний интеграл записан уже в каноническом виде.
б) 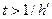 ; Сделаем замену переменной
; Сделаем замену переменной 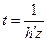 . Отсюда:
. Отсюда:
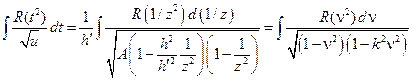 .
.
Получен канонический вид интеграла.
.
2°. 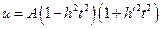 . Область определения подынтегрального выражения
. Область определения подынтегрального выражения
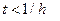 .
.
Замена: 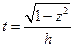 ;
; 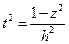 ;
; 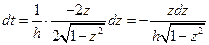 .
.
И, следовательно: 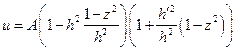 =
=
= 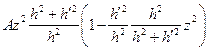 =
= 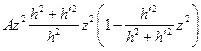 .
.
Тогда: 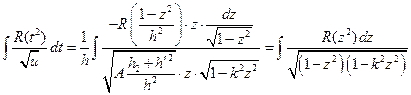 .
.
Вновь получен канонический вид интеграла.
3°. 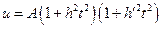 . Замена:
. Замена: 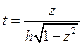 ;
; 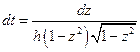 .
.
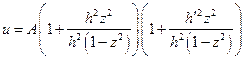 =
= 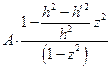 и получаем:
и получаем:
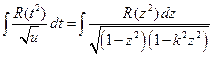 – канонический вид интеграла.
– канонический вид интеграла.
4°. 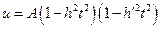 . Область определения:
. Область определения: 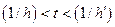 .
.
Производя замену 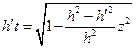 , получим:
, получим:
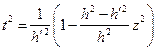 ;
; 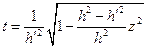 ;
; 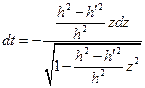 .
.
Теперь: 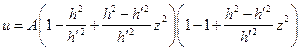 =
=
= 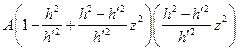 =
= 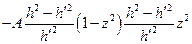 .
.
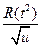 =
= 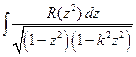 . Это вновь канонический вид исходного интеграла.
. Это вновь канонический вид исходного интеграла.
5°. 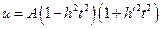 . Область определения подынтегрального выражения
. Область определения подынтегрального выражения
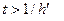 .
.
Выполним замену переменной: 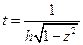 ;
; 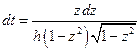 .
.
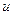 =
= 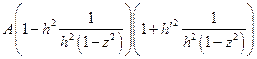 =
= 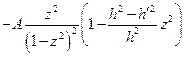 .
.
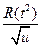 =
= 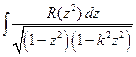 . Это снова канонический вид исходного интеграла.
. Это снова канонический вид исходного интеграла.
6°. 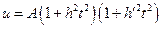 . Данное выражение всегда отрицательно и, следовательно, подынтегральная функция не определена.
. Данное выражение всегда отрицательно и, следовательно, подынтегральная функция не определена.
*. В итоге мы получили канонический вид эллиптического интеграла.
 2014-02-24
2014-02-24 1388
1388








