1. Пусть 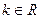 – фиксированное число. Рассмотрим отображение
– фиксированное число. Рассмотрим отображение
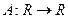
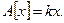
Это линейный оператор, причем таким образом устроена любая линейная функция на прямой.
2. Пусть 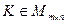 – фиксированная матрица размера
– фиксированная матрица размера 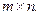 Рассмотрим отображение
Рассмотрим отображение
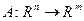
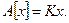
Это линейный оператор, причем любой линейный оператор, действующий из 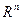 в
в 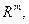 есть оператор умножения на матрицу размера
есть оператор умножения на матрицу размера 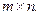
3. Пусть 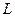 – линейное нормированное пространство над полем
– линейное нормированное пространство над полем 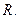 Рассмотрим тождественное отображение, которое по традиции обозначают буквой
Рассмотрим тождественное отображение, которое по традиции обозначают буквой 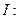
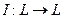
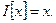
Это линейный оператор.
4. Пусть 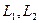 – линейные нормированные пространства над полем
– линейные нормированные пространства над полем 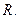 Рассмотрим нулевое отображение, которое все элементы пространства
Рассмотрим нулевое отображение, которое все элементы пространства 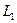 отображает в нулевой элемент пространства
отображает в нулевой элемент пространства 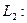
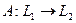
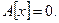
Это отображение также является линейным оператором.
В примерах 1 – 4 мы не приводим доказательство линейности, потому что оно слишком тривиально. Следующие примеры, хотя они тоже несложные, сопроводим проверкой соотношения линейности в форме (1.1) или (1.2).
5. Рассмотрим отображение
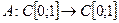
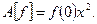
Проверим соотношения линейности в форме (1.2):
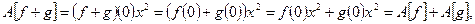
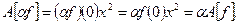
Следовательно, это отображение является линейным оператором.
6. Рассмотрим отображение
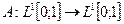
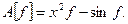
Проверим соотношения линейности в форме (1.2):
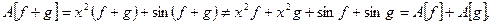
поскольку 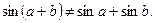 Второе соотношение (1.2) можно не проверять, если показано, первое уже не выполнено. Это отображение не является линейным оператором.
Второе соотношение (1.2) можно не проверять, если показано, первое уже не выполнено. Это отображение не является линейным оператором.
7. Рассмотрим отображение
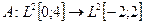
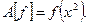
Проверим соотношения линейности в форме (1.2):
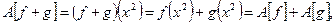
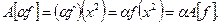
Значит, это отображение является линейным оператором (оператор замены переменной).
8. Рассмотрим отображение
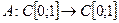
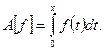
Значением этого отображения на функции 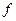 является интеграл с переменным верхним пределом, т.е. новая функция от переменной
является интеграл с переменным верхним пределом, т.е. новая функция от переменной 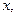 причем непрерывная по свойству непрерывности интеграла с переменным верхним пределом. Справедливость соотношения линейности в форме (1.1) опирается на линейность интеграла:
причем непрерывная по свойству непрерывности интеграла с переменным верхним пределом. Справедливость соотношения линейности в форме (1.1) опирается на линейность интеграла:
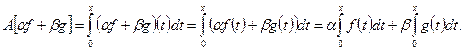
Таким образом, перед нами линейный оператор.
9. Рассмотрим отображение
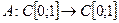
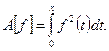
Это отображение похоже на предыдущий пример, но линейным оператором оно не является из-за операции возведения в квадрат функции 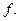 Не выполняются обе формулы (1.2), продемонтрируем на примере второй:
Не выполняются обе формулы (1.2), продемонтрируем на примере второй:
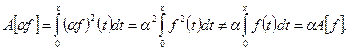
10. Рассмотрим отображение
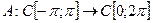
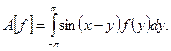
Это отображение является линейным оператором благодаря линейности интеграла. Проверим соотношение (1.1):
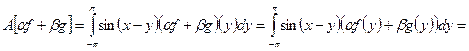
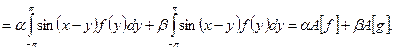
11. Рассмотрим отображение, которое сдвигает каждую непрерывную функцию на единицу вверх:
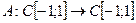
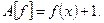
Оно не является линейным оператором, не выполняются соотношения (1.2), в частности, первое:
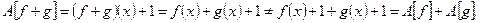
12. Рассмотрим отображение дифференцирования
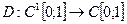
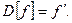
Дифференцирование, конечно, является линейным оператором, отсюда линейные свойства производной. Проверим формулу (1.1):
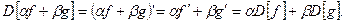
Упражнение: Проанализируйте, как связаны между собой понятия сжимающего отображения и линейного оператора для функций 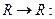 a) приведите примеры сжимающих функций, не являющихся линейными, и линейных функций, не являющихся сжимающими, а также функций, являющихся одновременно линейными и сжимающими; б) найдите общую формулу для линейных сжимающих функций
a) приведите примеры сжимающих функций, не являющихся линейными, и линейных функций, не являющихся сжимающими, а также функций, являющихся одновременно линейными и сжимающими; б) найдите общую формулу для линейных сжимающих функций 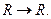
Упражнение: Найдите общую формулу для линейного сжимающего оператора 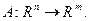
 2014-02-24
2014-02-24 4370
4370
