Раздел III. Теория линейных операторов и функционалов
Параграф 1. Линейный ограниченный оператор
Пусть 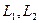 – линейные нормированные пространства над полем
– линейные нормированные пространства над полем 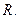 Отображение
Отображение 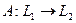 называется линейным оператором, если для любых
называется линейным оператором, если для любых 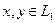 и
и 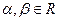
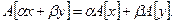 (1.1)
(1.1)
Соотношение (1.1) эквивалентно двум более простым соотношениям, проверять которые в отдельных случаях удобнее:
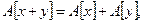
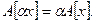 (1.2)
(1.2)
Упражнение: докажите, что любой линейный оператор отображает ноль в ноль, т.е. 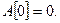
 2014-02-24
2014-02-24 409
409







