Асимметрия – это показатель симметричности / скошенности кривой распределения, а эксцесс определяет ее островершинность.
При левостронней асимметрии ее показатель является положительным и в распределении преобладают более низкие значения признака. При правостронней – показатель положительный и преобладают более высокие значения. У всех симметричных распеделений (в том числе и у нормального распределения) величина асимметрии равна нулю. Формула показателя асимметрии является следующей:
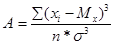
Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения 2 вершины (бимодальное распределение), то тогда эксцесс стремится к отрицательной величине. Показатель эксцесса определяется по формуле:
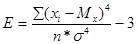
Распределение оценивается как предположительно близкое к нормальному, если установлено, что от 50 до 80 % всех значений располагаются в пределах одного стандартного отклонения от среднего арифметического, и коэффициент эксцесса по абсолютной величине не превышает значения равного двум.
Распределение считается достоверно нормальным если абсолютная величина показателей асимметрии и эксцесса меньше их ошибок репрезентативности в 3 и более раз.
Постановка задачи: определить или опровергнуть факт нормальности распределения показателей субтеста «аналогии» из Таблицы данных Приложения (взято первые 20 случаев).
| № | хi | xi-Mx | (xi-Mx)2 | (xi-Mx)3 | (xi-Mx)4 |
| -1 | -1 | ||||
| -1 | -1 | ||||
| -1 | -1 | ||||
| -5 | -125 | ||||
| -1 | -1 | ||||
| -2 | -8 | ||||
| -3 | -27 | ||||
| -3 | -27 | ||||
| -2 | -8 | ||||
| -1 | -1 | ||||
| S |
Для обработки данных понадобятся следующие последовательные шаги: вычисление Mx, s, А, Е по уже известным формулам. Необходимо также определение ошибок репрезентативности асимметрии и эксцесса:
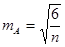 и
и 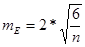

В нашем случае:
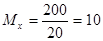
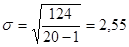
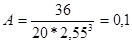
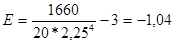
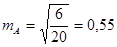
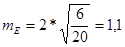
Как уже было сказано выше, принцип определения нормальности-ненормальности распределения является следующим:
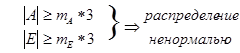
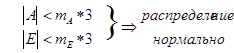
 В нашем случае:
В нашем случае:
 mA * 3 = 0,55 * 3 = 1,65 > ½А½
mA * 3 = 0,55 * 3 = 1,65 > ½А½
 mE * 3 = 1,1 * 3 = 3,3 > ½E½
mE * 3 = 1,1 * 3 = 3,3 > ½E½
Поскольку оба показателя не превышают в 3 раза свою собственную ошибку репрезентативности, можно заключить, что распределение показателей субтеста «аналогии» соответствует нормальному.
 2014-02-24
2014-02-24 5871
5871
