Особенности кривой нормального распределения

1. Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению 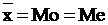(Хср = Mo = Me), ее величина равна

2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от Хср, тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной х от Хср равновероятны.

3.Кривая имеет две точки перегиба, находящиеся на расстоянии ± s от Хср.

4. При Хср = const с увеличением s кривая становится более пологой. При s = const с изменением Хср кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.

5. В промежутке находится 68,3% всех значений признака. В промежутке находится 95,4% всех значений признака. В промежутке находится 99,7% всех значении признака.

Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другими.

Содержание отчета

1. Исходное задание (с таблицей).

2. Расчетная часть (расчеты свести в таблицу).

3. Построить график распределения, где ось ординат - значения частот fi, а ось абсцисс - значения признака Xi. На графике отметить среднее значение изучаемого признака, моду и медиану.

4. Аналитическая записка.

Контрольный пример

Задача 1

Имеются следующие данные о заработной плате рабочих.

Заработная плата в руб.	400-500	500-600	600-700	700-800	800-900
Число рабочих

Требуется определить:

1. Среднюю заработную плату в цехе.

2. Модальное и медианное значение заработной платы.

3. Среднее квадратическое отклонение.

4. Дать экономическую интерпретацию полученным результатам.

 

Расчетная часть

Заработная плата	Количество человек (Частоты)	Накопленные частоты	Середина интервала	Промежуточные расчеты
	fi	Si	Хi	fi*Хi	(Хi-Хср)2 fi
400-500					66170,79
500-600					24723,42
600-700					3276,056
700-800					1828,688
800-900					20381,32
					116380,28

 

Средняя заработная плата =537500/760 = 707,2 руб.

Модальное значение = 700+100*(235-175)/((235-175)+(235-200)) =737,7 руб.

Полусумма накопленных частот=760/2 = 380

Медианное значение = 700+100*(380-325) / 235 = 723,3 руб.

Дисперсия

Среднее квадратическое отклонение 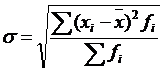= 12,37 руб.

Средняя ЗП=707 руб. Мода = 738 руб. Медиана = 723 руб.

 

Для сравнительного анализа степени асимметрии нескольких распределений рассчитаем относительный показатель асимметрии As.

Величина показателя асимметрии A_s = -1,3 отрицательна и указывает на наличие левосторонней асимметрии. При левосторонней асимметрии между показателями центра распределения существует соотношение:

Применение показателя A_s дает возможность не только определить степень асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений и рассчитывается по формуле:

Отношение поэтому асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

 

АНАЛИТИЧЕСКАЯ ЗАПИСКА

Средняя заработная плата в цехе равна 707 руб.

Структурные средние:

Модальное значение зарплаты в цехе составило 738 руб.

Медианное значение зарплаты в цехе составило723 руб.

При анализе рассчитанных показателей видно, что величина показателя асимметрии A_s = -1,3 отрицательна и указывает на наличие левосторонней асимметрии, что также подтверждается неравенствами:

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, что изучаемое распределение нельзя отнести к нормальному типу.

 

Задача 2

По данным ГКС известно распределение населения по величине среднедушевых денежных доходов.

Необходимо рассчитать:

Среднедушевой денежный доход на основе средней арифметической, моды, медианы.

Дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Децильный коэффициент дифференциации доходов, ДКДД.

Коэффициент Джини (показатель концентрации доходов) G. Построить кривую Лоренца.

Дать экономическую интерпретацию полученных результатов.

 

Среднемесячный душевой доход, тыс. руб. (с 1998 г. - руб.)	Млн.человек	В процентах
Все население, в том числе со среднедушевыми денежными доходами в месяц, тыс. руб.1)	147,9	147,6	147,1	146,7	146,3
до 400,0	70,7	38,1		22,1	5,2	47,8	25,8
400,1-600,0	34,6	33,7	28,5	27,8	12,4	23,4	22,8
600,1-800,0		25,1	23,7	25,2	16,7	12,8
800,1-1000,0	10,1	16,9	17,8	19,6	17,4	6,9	11,4
1000,1-1200,0	5,5		12,8	14,3	16,1	3,7	7,5
1200,1-1600,0	4,9		15,8	17,6	25,8	3,3	8,1
1600,1-2000,0	1,7	5,4	8,3		17,6	1,2	3,7
свыше 2000,0	1,4	5,4	11,2	11,1	35,1	0,9	3,7

 

РЕШЕНИЕ (по данным 1995 года).

1.1. Вычисление средней арифметической:

 

Среднемесячный душевой доход,	Численность населения %,	Середина интервала	Сумм. Доход по группам	Накоплен-ные частоты	(x i - хср)2*fi
руб.	f i	x i	xi fi	Si = f i
до 400,0	47,8			47,8
400,1-600,0	23,4			71,2
600,1-800,0	12,8			84,0
800,1-1000,0	6,9			90,9
1000,1-1200,0	3,7			94,6
1200,1-1600,0	3,3			97,9
1600,1-2000,0	1,2			99,1
свыше 2000,0	0,9			100,0
Всего		-		-

 

1.1 Расчет средней арифметической.

1.2. Вычисление моды:

Наибольшую частоту (47,8%) имеет интервал (до 400 руб.). Поэтому имеем:

 

 

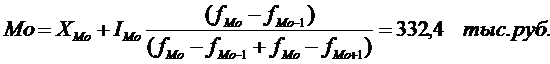
где Х_Мо = 200 - начало модального интервала;

I_МО = 200 - величина модального интервала;

f_МО-1, f_МО, f_МО+1 - частоты предмодального, модального и послемодального интервала (соответственно равны 47,8%, 0%, 23,4%).

 

1.3. Определение медианы:

По накопленным частотам, 50-й процент достигается в интервале (400-600), т.к. 71,2% впервые превышает 50%:

 

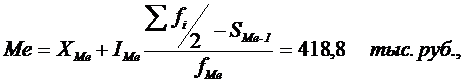
где:

Хме -=400 - нижняя граница варианты медианного интервала,

Iме -=200 - величина медианного интервала,

- полусумма накопленных частот,

S_Ме-1 - =47,8% -накопленные частоты перед медианным интервалом,

f_Ме - =23,4% -частота медианного интервала.

 

1.4. Расчет дисперсии.

Д=119987,8 тыс. руб.²

Среднее квадратическое отклонение=346,4 тыс. руб.

 

1.5. Расчет коэффициента вариации.

Изучаемая совокупность не является однородной, т.к. γ >>30-33%)

 

1.5. Определение децильного коэффициента дифференциации доходов (ДКДД).

 

ДКДД =D9 / D1

D 1 = Х н+ h (10 % - S (D1-1)) / f D 1 = 241,84 тыс. руб.

D 1- первая дециль находится в первом интервале (до 400)

D 9 - девятая дециль находится в (800-1000)

Нижняя граница первого интервала -60

D 9 = Х н +h (90 % - S (D9-1)) / f D 9 = 973,9тыс. руб.

Нижняя граница девятого интервала -800

ДКДД =D9 / D1 = 4,0 раз.

 

1.6. Определение коэффициента Джини (показателя концентрации доходов) G

Среднемесячный душевой доход, руб.	Численность населения %,	Середина интервала	Суммарный доход по группам	Суммарный доход по группам в %	Накопленные частоты населения	Накопленные итоги суммарного дохода %
	f i	x i	xi fi
до 400,0	48%			27%	48%	27%
400,1-600,0	23%			22%	71%	48%
600,1-800,0	13%			17%	84%	65%
800,1-1000,0	7%			11%	91%	76%
1000,1-1200,0	4%			8%	95%	84%
1200,1-1600,0	3%			9%	98%	92%
1600,1-2000,0	1%			4%	99%	96%
свыше 2000,0	1%			4%	100%	100%
Всего	100%	-		100%

 

G=((47,8*26040+71,2*35000+84*41210+90,9*45280+94,6*49900+ 97,9*52060+ 99,1*54040) - (71,2*14340+84* 26040+90,9*35000 +94,6 * 41210 +97,9 *45280+99,1*49900+100*52060)) / 10000

G=0,299

Аналитическая записка.

Результаты анализа среднемесячного душевого дохода в РФ за 1995 год позволяют сделать следующие выводы:

Среднемесячный душевой доход составляет 540,4 тыс. руб. При этом большая часть населения имеет доход 332,4 тыс. руб., а половина населения РФ имеют доходы, не превышающие 418,8 тыс. руб.

Расчет коэффициента вариации, равного приводит к выводу о том, что изучаемая совокупность, т. е. Население РФ в целом, не является однородной (γ>>>30-33%)

Определение децильного коэффициента дифференциации доходов (ДКДД) как отношение минимального дохода 10% наиболее обеспеченных к максимальному доходу 10% самых бедных свидетельствует о значительном расслоении населения по доходам, что подтверждает и рассчитанный коэффициент концентрации доходов (коэффициент Джини).