Пример
1)
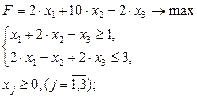
Решение:
Сведем ограничения типа ≥ к ограничениям ≤ умножением на -1.
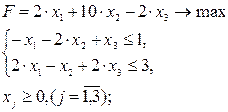
Так на все переменные наложены условия неотрицательности, то в двойственной задаче все ограничения будут являться неравентвами.
Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит три переменные, то двойственная задача будет иметь три ограничения.
Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.
Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.
Учитывая указанные выше правила, имеем двойственную задачу:
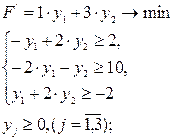
2)
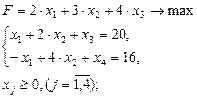
Решение:
Так как на переменные наложены условия неотрицательности, то ограничения двойственной задачи будут ограничениями-неравенствами. Так как ограничения прямой задачи являются равенствами, то на переменные двойственной задачи не накладывается условие неотрицательности.
Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит четыре переменные, то двойственная задача будет иметь четыре ограничения.
Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.
Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.
В результате получим следующую модель двойственной задачи:

Анализ решения линейной задачи разберем на примере задачи определения оптимального ассортимента выпускаемой продукции.
Пусть задача имеет следующую математическую модель
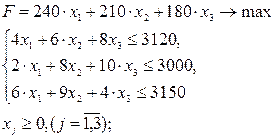
Пусть данные на листе Excel размещены следующим образом
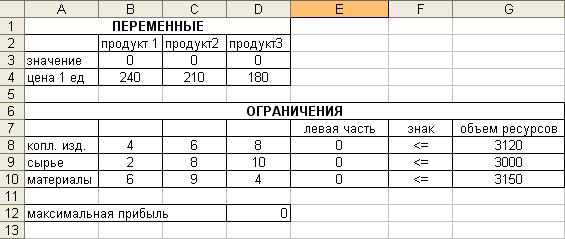
Результат решения:
х1=397,5; х2=0; х3=191,25 Fmax=129 825.
По результатам решения формируется три отчета: по результатам, по устойчивости, по пределам.
 2014-02-24
2014-02-24 2193
2193
