В данном классе игр нижняя цена игры строго меньше верхней 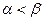 .
.
Введем понятие смешанной стратегии. Смешанная стратегия – комбинация чистых стратегий с вероятностями выбора 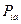 :
:
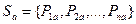 ;
; 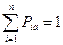 .
.
Оптимальная смешанная стратегия: 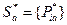 .
.
Для любой матрицы 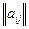 можно определить оптимальную смешанную стратегию:
можно определить оптимальную смешанную стратегию: 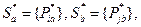 такую, что выигрыш участника
такую, что выигрыш участника  , определяемый в соответствии с выражением:
, определяемый в соответствии с выражением:
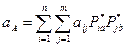 ,
,
будет в интервале 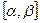 (для участника
(для участника  это проигрыш
это проигрыш 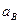 ).
).
Теорема о минимаксе. В матричной игре без седловой точки 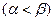 существует точка равновесия такая, что выигрыш участника
существует точка равновесия такая, что выигрыш участника  находится в интервале
находится в интервале  , и оптимальные решения для участников находятся из условий:
, и оптимальные решения для участников находятся из условий:
для  –
–  из условия
из условия 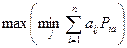 ,
,
для  –
– 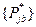 из условия
из условия 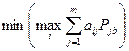 ,
,
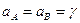 – цена игры.
– цена игры.
Доказательство теоремы будет рассмотрено далее.
Определение 2 (активные стратегии). Активные стратегии для участника  – это те стратегии из множества чистых
– это те стратегии из множества чистых 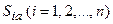 , для которых
, для которых 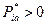 .
.
Утверждение 1. Если участник  придерживается оптимальной смешанной стратегии, то его выигрыш не зависит от стратегии участника
придерживается оптимальной смешанной стратегии, то его выигрыш не зависит от стратегии участника  в пределах активных стратегий участника
в пределах активных стратегий участника  .
.
Доказательство. Пусть участник  придерживается оптимальной смешанной стратегии, а
придерживается оптимальной смешанной стратегии, а  – произвольной смешанной. Тогда выигрыш участника равен:
– произвольной смешанной. Тогда выигрыш участника равен:
 .
.
Пусть 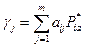 – выигрыш участника
– выигрыш участника  , если участник
, если участник  придерживается чистой стратегии
придерживается чистой стратегии 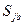 , и одновременно
, и одновременно 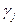 – проигрыш для участника
– проигрыш для участника  , тогда
, тогда
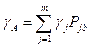 . (2.1)
. (2.1)
Поскольку чистая стратегия 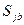 не является оптимальной стратегией для участника
не является оптимальной стратегией для участника  , то
, то 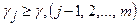 , где
, где 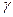 – цена игры.
– цена игры.
Запишем (2.1) с учетом этого неравенства:
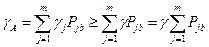 .
.
С учетом, что  получаем нестрогое неравенство
получаем нестрогое неравенство 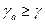 . Но так как участник B осуществляет выбор на множестве активных стратегий, а
. Но так как участник B осуществляет выбор на множестве активных стратегий, а 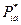 – оптимальная стратегия для A, то
– оптимальная стратегия для A, то 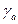 не может быть больше
не может быть больше 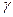 . Следовательно
. Следовательно 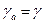 .
.
2.3.1. Решение матричных игр 2´2
Каждый из участников имеет по две чистые стратегии. Матрица выигрышей для A имеет вид:
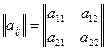 .
.
Элементы матрицы таковы, что 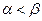 , т.е. седловой точки нет.
, т.е. седловой точки нет.
В качестве решения игры необходимо получить смешанные стратегии  .
.
На основе доказанного выше утверждения для оптимальной стратегии участника  будет выполняться следующее тождество:
будет выполняться следующее тождество:
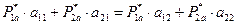 .
.
Учитывая, что 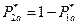 :
:
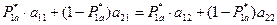 .
.
Откуда получим
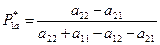 , (2.2)
, (2.2)
 . (2.3)
. (2.3)
Для определения 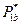 также составим уравнение:
также составим уравнение:
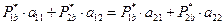 ;
;
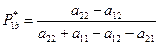 ; (2.4)
; (2.4)
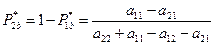 . (2.5)
. (2.5)
Цена игры (выигрыш для участника ) будет равна:
) будет равна:
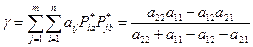 .
.
Для того чтобы решения (2.2), (2.3), (2.4), (2.5) были положительными числами (вероятностями), необходимо, чтобы для элементов матрицы 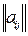 выполнялись следующие неравенства:
выполнялись следующие неравенства:
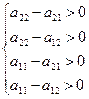 или
или 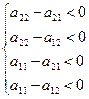 .
.
Пример задачи. Правила игры. Каждый из участников имеет две чистые стратегии:
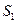 – выбрать число 1,
– выбрать число 1,
 – выбрать число 2.
– выбрать число 2.
Если сумма у двух участников окажется четным числом, то выигрыш  составит эту сумму. Если же сумма окажется нечетной, то выигрывает участник
составит эту сумму. Если же сумма окажется нечетной, то выигрывает участник  .
.
Данные правила отражены в следующей платежной матрице:
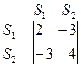 .
.
Найдем оптимальные смешанные стратегии для каждого из участников
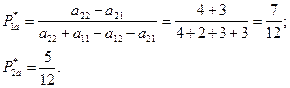
Для участника  решением будет:
решением будет:
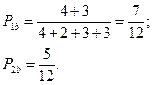
Цена игры равна: 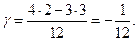
Поскольку 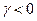 , выигрывает участник В; из этого можно сделать вывод, что правила игры несправедливы.
, выигрывает участник В; из этого можно сделать вывод, что правила игры несправедливы.
Отметим, что при выборе участником В оптимальной смешанной стратегии его выигрыш 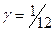 не будет зависеть от действий противника. Это следует из утверждения 1, поскольку у участника А обе чистые стратегии активные.
не будет зависеть от действий противника. Это следует из утверждения 1, поскольку у участника А обе чистые стратегии активные.
Графическая интерпретация решения игры 2´2. Построим зависимость выигрыша участника  от
от 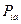 (рис. 2.1),
(рис. 2.1),
 где
где 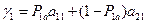 – выигрыш участника А, если участник придерживается чистой стратегии
– выигрыш участника А, если участник придерживается чистой стратегии 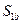 ,
, 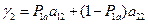 – если участник придерживается чистой стратегии
– если участник придерживается чистой стратегии 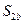 .
.
Приравняв g 1 и g 2, получим оптимальное значение 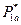 , которое соответствует
, которое соответствует 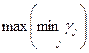 , т.е.
, т.е.  максимизировал свой выигрыш.
максимизировал свой выигрыш.
 Теперь рассмотрим решение игры с позиции участника
Теперь рассмотрим решение игры с позиции участника  . Построим зависимость его проигрыша от
. Построим зависимость его проигрыша от 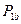 (рис. 2.2),
(рис. 2.2),
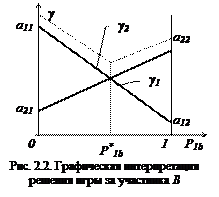 где
где 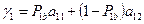 – проигрыш участника В, если участник придерживается чистой стратегии
– проигрыш участника В, если участник придерживается чистой стратегии  ,
, 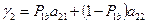 – если участник придерживается чистой стратегии
– если участник придерживается чистой стратегии 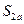 .
.
Оптимальное значение 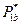 получается из условия
получается из условия 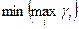 , т.е. он минимизирует проигрыш.
, т.е. он минимизирует проигрыш.
2.3.2. Решение матричных игр 2´m графоаналитическим методом
Если участник  имеет 2 чистые стратегии, а
имеет 2 чистые стратегии, а  –
– 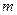 чистых стратегий, то матрица выигрышей для
чистых стратегий, то матрица выигрышей для  имеет вид:
имеет вид:
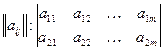 .
.
 Построим зависимость выигрыша участника
Построим зависимость выигрыша участника  от
от  при чистых стратегиях участника
при чистых стратегиях участника
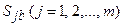 :
:
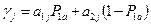 .
.
Оптимальное  находим из условия
находим из условия 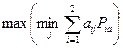 (рис. 2.3). Найденному
(рис. 2.3). Найденному 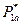 соответствуют две чистые стратегии участника
соответствуют две чистые стратегии участника  , которые будут для него активными. Таким образом, игру
, которые будут для него активными. Таким образом, игру 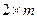 сводим к игре
сводим к игре 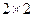 .
.
Если несколько прямых пересекаются в одной точке, то нужно брать две стратегии, которые имеют более острый угол, это обеспечит более устойчивое решение.
Пример. Дана платежная матрица, необходимо найти оптимальные смешанные стратегии:
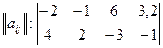 .
.
Строим зависимость 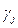 от
от  :
: 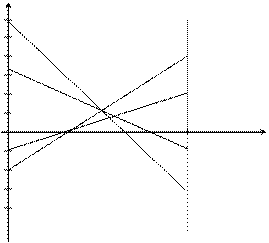
|
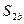 и
и 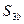 по
по
нове й инженерно-физический институт (государственный книверситет), 2007. принципу 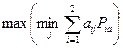 .
.
Переходим к матрице 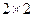 -
- 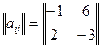 и рассчитываем оптимальные
и рассчитываем оптимальные 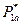 и
и 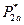 :
:
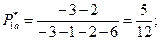
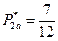 . Решением игры для участника В является:
. Решением игры для участника В является:
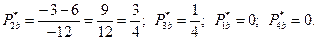
2.3.3. Решение матричных игр n´2 графоаналитиским методом
Участник  имеет
имеет 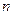 чистых стратегий, а
чистых стратегий, а  – 2 чистые стратегии, платежная матрица имеет вид:
– 2 чистые стратегии, платежная матрица имеет вид:
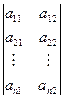 .
.
Построим зависимость проигрыша участника  от
от 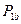 при чистых стратегиях
при чистых стратегиях 
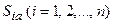 :
:
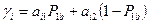 .
.
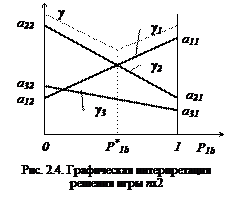
Оптимальное 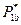 находим из условия
находим из условия 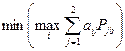 , после чего выделяем две активные стратегии для участника
, после чего выделяем две активные стратегии для участника  и переходим к игре
и переходим к игре 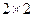 .
.
2.3.4. Решение матричных игр n´m
Задана 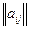 – матрица выигрышей для игрока
– матрица выигрышей для игрока  . Необходимо найти оптимальные смешанные стратегии:
. Необходимо найти оптимальные смешанные стратегии:
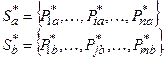
 2014-02-24
2014-02-24 2251
2251
