Рис.2. Пример системы
Рис.1. Спектр моделей
Физические модели часто называют натурными, так как внешне они напоминают изучаемую систему. Они могут быть выполнены в уменьшенном масштабе (например, модель солнечной системы) и в увеличенном (например, модель атома) – это уже масштабируемые модели.
Аналоговые модели – это модели, в которых свойство реального объекта представляется другим свойством, аналогичным по поведению объекта. Примером подобного типа моделей может служить аналоговая ЭВМ, в которой изменение напряжения может отображать изменение какого-то параметра, например, температуры.
График представляет собой аналоговую модель другого вида. Здесь расстояние отображает характеристики объекта. График показывает соотношение между различными количественными характеристиками и может предсказывать, как будут изменяться одни величины при изменении других.
Различного рода схемы также являются аналоговыми моделями (например, структурная схема какой-либо организации).
Математические модели – это совокупность математических объектов и отношений между ними, которая приближённо описывает некоторые свойства объекта или процесса. Таким образом, математическая модель является упрощением реальной ситуации и представляет собой абстрактный, формально описанный объект, изучение которого возможно математическими методами. Математические модели являются основой для создания имитационных моделей.
Имитационная модель – это программа, реализующая на машинном языке описание моделируемой системы (математической модели).
1.3. Основные сведения о математических моделях
Каждая математическая модель представляет собой упорядоченную комбинацию таких составляющих как компоненты, переменные, параметры, функциональные зависимости и ограничения.
Под компонентами модели понимаются составные части, которые при соответствующем объединении образуют систему. Компонентами могут быть либо неделимые структурные образования, которые называются элементами модели, либо составные, являющиеся подсистемами модели.
Топология модели – это отношение компонентов, образующих систему. Это отношение должно быть определено на множестве переменных модели.
Рассмотрим простейшую систему (рис.2).
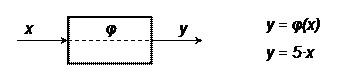

Входы и выходы системы (x и y) называют переменными системы, а число 5 является параметром системы и характеризует свойства функциональной зависимости, связывающей входную переменную x с выходной переменной y.
Различают экзогенные и эндогенные переменные. Экзогенными переменными называют входные переменные, они порождаются вне изучаемой системы и являются результатом действия внешних причин. Эндогенными называются переменные, возникающие в системе в результате действия на неё экзогенных переменных. Эндогенные переменные также называют выходными или координатами состояния.
Функциональные зависимости описывают поведение переменных и параметров в пределах компонента или всей системы. Обычно они устанавливают внутренние отношения между экзогенными и эндогенными переменными либо между переменными и зависимыми от них параметрами:
y = φ(p,x);
p = ψ(x,y).
Функции φ называют операторными (или просто операторами), а функции ψ – параметрическими.
В общем случае x, y и p рассматриваются как процессы, то есть функции времени x(t), y(t) и p(t). Для x и y аргумент времени t можно опускать.
Y = φ[P(t),X],
где Х, Y – векторы входных и выходных переменных модели;
Р – матрица параметров модели.
К ограничениям относят области изменения переменных и параметров модели. Следует отметить, что даже небольшие участки реального мира слишком сложны для описания, поэтому при моделировании необходимо решать задачу выбора достаточной степени приближения. Во многом принятие тех или иных ограничений зависит от назначения модели.
1.4. Классификация математических моделей
Математические модели делятся на следующие группы.
1. В зависимости от характера отображаемых свойств объекта модели могут быть функциональными и структурными.
Функциональные модели отображают процессы функционирования объекта. Чаще всего они имеют форму системы уравнений.
Структурные модели могут иметь форму матриц, графов, списков векторов и выражают взаимное расположение элементов в пространстве. Эти модели обычно используют в случаях, когда задачи структурного синтеза удаётся ставить и решать, абстрагируясь от физических процессов в объекте. Они отражают структурные свойства проектируемого объекта.
Также для получения статического представления моделируемой системы может быть использована группа методов, называемых схематическими моделями. Это методы анализа, включающие графическое представление работы системы (например, технологические карты, диаграммы, блок-схемы и т.п.).
2. По способам получения функциональных математических моделей они делятся на теоретические и формальные.
Теоретические модели получаются на основе изучения физических закономерностей. Структура уравнений и параметры моделей в этом случае имеют определенное физическое толкование.
Формальные модели получаются на основе проявления свойств моделируемого объекта во внешней среде, то есть используют рассмотрение объекта как «черного ящика».
Теоретический подход позволяет получать модели более универсальные, справедливые для более широких диапазонов изменения внешних параметров. Формальные модели более точны в точке пространства параметров, в которой производились измерения.
3. По форме связей между выходными, внутренними и внешними параметрами модели делятся на алгоритмические и аналитические.
Алгоритмические модели записываются в виде систем уравнений.
Аналитические модели записываются в виде зависимостей выходных параметров от внутренних и внешних.
4. По особенностям операторов φ математические модели делятся на:
· стационарные и нестационарные;
· статические и динамические;
· линейные и нелинейные;
· со сосредоточенными и распределёнными параметрами;
· непрерывные и дискретные.
Полное наименование модели может включать в себя совокупность перечисленных признаков. Например, классическая теория автоматического регулирования в основном оперирует линейными стационарными динамическими моделями с сосредоточенными параметрами. В то же время для задач оперативного управления в АСУТП характерно применение статических нелинейных, часто нестационарных моделей.
1.5. Стационарные и нестационарные модели
Модель называется стационарной, если вид оператора φ и её параметры Р не изменяются с течением времени, то есть, когда справедливо равенство
φ [ P(t), X ] = φ [ P(t + τ), X ].
В этом случае можно из записи функции опустить аргумент t для параметров:
Y = φ [ P, X ].
Например, y = 2·x.
Если же параметры модели изменяются во времени, то модель называется параметрически нестационарной:
Y = φ [ P(t), X ].
Например, 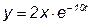 .
.
В самом общем случае нестационарности может оказаться зависимым от времени и вид функции:
Y = φ [ t, P(t), X ].
Например, 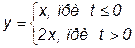 .
.
1.6. Статические и динамические модели
В основе такого разделения типов моделей лежат особенности движения исследуемого объекта как материальной системы. Говоря о моделях с позиций задач управления, следует отметить, что понятие пространства, обычно понимаемое в геометрическом смысле и относящееся к механическим системам, не совсем подходит для широкого класса технологических процессов. Более того, для многих объектов управления характерно не взаимное перемещение элементов, а изменение их внутреннего состояния. Поэтому под пространством здесь понимается именно пространство состояний объекта и его модели. Тогда положение объекта или прогноз его положения по модели можно оценить с помощью координат состояния Y, относящихся к эндогенным переменным.
Элементами вектора Y обычно являются контролируемые технологические параметры, такие как расход среды, давление, температура, влажность, вязкость и т.п. Применительно к макросистемам состояние объектов обычно выражают посредством законов термодинамики. Первый закон термодинамики говорит о неуничтожимости материи и её движения и записывается через совокупность законов сохранения массы, энергии и количества движения. Второй закон термодинамики отражает направленность реальных процессов и связан с оценкой изменения энтропии системы при изменении её состояния.
Так, уравнение материального баланса системы (закон сохранения массы) можно записать в следующем виде:
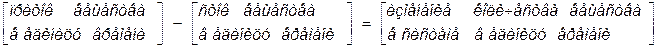
или в виде математической формулы:
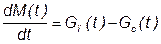 .
.
Рассмотрим в качестве примера бак с жидкостью, как простейшую техническую систему (рис.3).
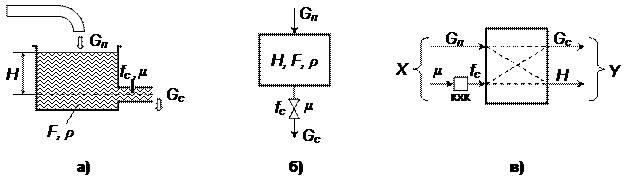 |
 2014-02-09
2014-02-09 894
894








