Лекция №4. Рис.5. Кусочно-линейная аппроксимация

Рис.5. Кусочно-линейная аппроксимация

Рис.4. Переходные процессы в системе

Временные интервалы (t₀-t₁), (t₂-t₃), (t₄-t₅) соответствуют состояниям равновесия в баке, а интервалы (t₁-t₂), (t₃-t₄) отражают переходные процессы, вызванные изменением входных переменных.

1.7. Линейные и нелинейные модели

Принято считать функцию одного аргумента L(x) линейной, если выполняется следующее условие:

.

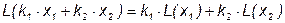Аналогично понимается и линейность функций нескольких переменных.

Линейным функциям присуще использование только операций алгебраического суммирования и умножения переменой на постоянный коэффициент. С этой точки зрения, полученные в предыдущем пункте модели следует считать нелинейными, так как в них присутствуют операции возведения в квадрат и деление переменных, а также умножение выражений содержащих переменные.

Статические модели, как правило, являются нелинейными. С вычислительной точки зрения проблем расчёта таких алгебраических выражений не существует. Точные решения дифференциальных уравнений, составляющих динамические модели, известны лишь для некоторых простейших случаев. Чаще всего при решении дифференциальных уравнений используют численные методы, являющиеся приближёнными. Однако сложное дифференциальное выражение можно упростить, произведя его линеаризацию, и, тем самым, переведя его в класс функций, который очень хорошо изучен и нередко уже имеет набор готовых решений.

Линеаризация основана на разложении нелинейной функции в ряд Тейлора в окрестностях заданных исходных значений переменных. При этом ограничиваются только линейными членами разложения.

Пусть необходимо получить линеаризованную динамическую модель бака с жидкостью. Исходное состояние равновесия системы соответствует моменту времени t₀. Для оценки значений координат состояния в начальном состоянии равновесия можно воспользоваться статической моделью:

;

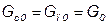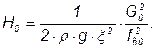
Основную нелинейность в динамическую модель объекта вносит соотношение

.

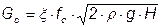Разложим его в ряд Тейлора, ограничиваясь только линейными членами:

,

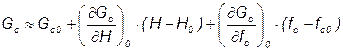где 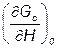и 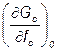– частные производные по входным переменным в начальный момент времен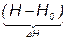и;

и 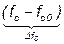– приращения входных переменных: H=H₀+ΔH, f_c=f_c0+Δf_c.

Определим коэффициенты ряда Тейлора:

;

.

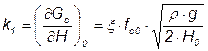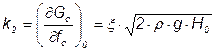В итоге получаем первое линеаризованное уравнение, записанное в приращениях:

,

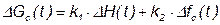где .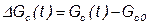

Теперь рассмотрим второе уравнение

.

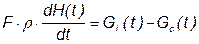Перепишем его в следующем виде:

.

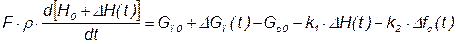Принимая во внимание, что 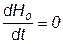и 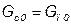, получаем второе линеаризованное дифференциальное уравнение:

.

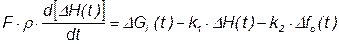Считая, что y₁ = ΔG_c, y₂ = ΔH, x₁ = ΔG_п, x₂ = Δf_c, линеаризованную модель бака с жидкостью можно представить следующей системой уравнений:

,

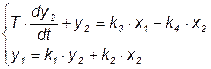где , , .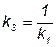

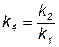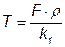Коэффициенты k_i и Т являются параметрами линеаризованной модели и зависят от состояния равновесия, предшествующего переходному процессу. Поэтому модель требует пересчёта её параметров в случае изменения исходного состояния моделируемого объекта (Н₀; G_c0).

При описании объекта, работающего в переменных режимах с широким диапазоном изменения своего состояния, пренебрегать переменностью параметров уже нельзя. Поэтому динамическая модель в этом случае должна быть дополнена моделью зависимости параметров от влияющих факторов (экзогенных переменных).

В случае необходимости моделирования объекта в широком диапазоне режимов при существенном изменении крутизны характеристик переходят к их кусочно-линейной аппроксимации, осуществляя линеаризацию на отдельных участках изменения координат (рис.5).

При этом нелинейный объект описывается совокупностью линейных уравнений и логических зависимостей, определяющих зону действия каждого линейного выражения:

.

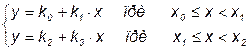1.8. Модели со сосредоточенными и распределёнными параметрами

Следует отметить, что корректнее было бы использовать понятие «координата состояния» вместо «параметр», однако такое название является устоявшимся.

Существуют такие объекты, для которых некоторые координаты состояния (технологические параметры) требуют ориентации в геометрическом пространстве.

Рассмотрим для примера участок трубы, в которой вода нагревается подводимым снаружи теплом (рис.6).