2014-02-09
649
Рис.3. Бак с жидкостью
а) физическая схема; б) структурная схема; в) эквивалентная схема
Основные технологические координаты и параметры:
Gп – расход жидкости, поступающей в бак (независимый приток);
Gс – расход жидкости, вытекающей из бака (зависимый сток);
Н – высота уровня жидкости над сливным отверстием;
fc – площадь проходного сечения сливного отверстия;
μ – положение регулирующего клапана на стоке жидкости из бака;
F – площадь поперечного сечения бака (постоянный параметр);
ρ – плотность жидкости (постоянный параметр);
КХК – конструктивная характеристика клапана.
Требуется изучить поведение объекта в условиях равновесия, то есть при неизменности координат состояния Н и Gс во времени. В равновесном состоянии в баке не будет происходить изменения количества вещества:
.
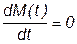Тогда уравнение материального баланса примет следующий вид:
.
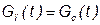С другой стороны, понятие равновесия с математической точки зрения выражается равенством нулю всех производных координат состояния:
|
|
|
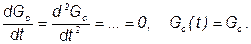
Соответственно,
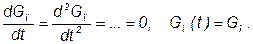
В итоге получаем:
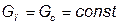
В соответствии с законом гидродинамики, отражающим закон сохранения количества движения, имеем:
,
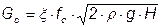где ξ – расходный коэффициент.
Подставляя это выражение в уравнение материального баланса, получаем возможность вычислять (прогнозировать, моделировать) высоту уровня жидкости в баке:
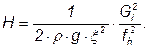
Таким образом, математическая модель рассматриваемой системы, находящейся в состоянии равновесия, может быть представлена в следующем виде:
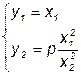или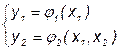 
,
где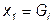 
, 
, 
, 
, 
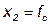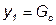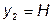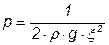– параметр модели.
Такую модель принято называть статической. Она описывает объект, находящийся в статичном положении, то есть в положении равновесия.
Рассмотрим тот же объект в общем случае. Запишем соотношение, позволяющее определить количество жидкости в баке, находящейся над плоскостью сливного отверстия:
.
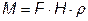Считая площадь поперечного сечения бака F и плотность жидкости ρ постоянными, запишем уравнение материального баланса:
.
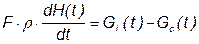Подставляя сюда выражение для Gс , получим дифференциальное уравнение:
,
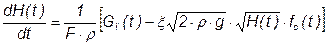которое в обобщённой форме может быть выражено следующим образом:
.
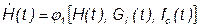Соотношение для расхода жидкости
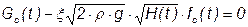
в обобщённом виде записывается как:
.
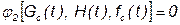В итоге получаем систему уравнений с двумя неизвестными:
.
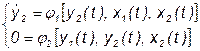Такая система является динамической моделью бака с жидкостью. При этом динамика связана с изменением состояния системы. Рассмотренная ранее статическая модель является частным случаем динамической.
В реальных условиях переходные (динамические) и статические состояния объекта обычно чередуются друг с другом (рис.4).
|
|
|
 |
