Лекция №7. Рис.10. Этапы формирования модели

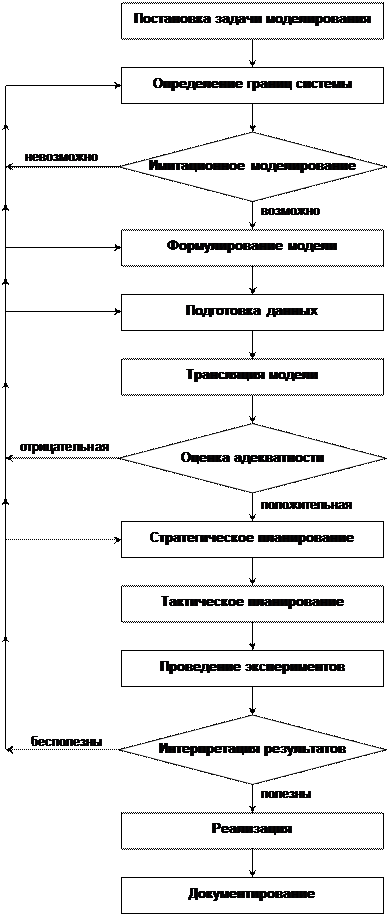
Рис.10. Этапы формирования модели

Рис.9. Типы компонентов

В компонентах преобразования один или несколько входных сигналов преобразуются в один или несколько выходных сигналов.

В компонентах сортировки один или несколько входных сигналов распределяются (сортируются) по двум или нескольким разным выходам.

В компонентах обратной связи входной сигнал некоторым образом изменяется в зависимости от выходного сигнала.

Степень сложности, с которой задаётся структура компонентов системы, зависит от исходного знания системы. Если природа исследуемого процесса совершенно неизвестна или известна слабо, то мы имеем дело с идентификацией «черного ящика». В этом случае систему описывают линейными или нелинейными уравнениями передаточных характеристик.

В некоторых случаях можно знать многое о природе процесса и не знать лишь значения некоторых параметров. Это, так называемая, задача идентификации «серого ящика».

Основными методами конструирования математических моделей являются:

1. Аксиоматический метод. Суть этого метода состоит в том, что в самом начале формулируются некоторые утверждения относительно реальных объектов, которые представляются в виде набора математических выражений – аксиом. Далее на их основании делают определенные выводы.

Достоинством этого метода является то, что он обеспечивает в пределах принятых аксиом непротиворечивые выводы относительно существенных свойств объекта. Основным недостатком метода является то, что сами аксиомы не проверяются непосредственно в эксперименте.

2. Метод уравнений элементов. Обычно этот метод используется тогда, когда надо составить математическую модель объекта на основе свойств его частей или когда из заданного набора элементов необходимо составить сложный объект и определить его свойства.

Обычно сложная система разделяется на подсистемы и элементы таким образом, чтобы стала доступной формализация каждого элемента и взаимодействий между ними.

В зависимости от характера элементов системы (детерминированные, стохастические, с непрерывным или дискретным временем и т.д.) для их описания используются те или иные типичные математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, переключательные сети, графовые модели, и т.д.

Однако в действительности бывает, что объект проявляет ряд свойств, которые не сводятся к совокупности свойств его элементов.

3. Метод идентификации. Суть метода состоит в том, чтобы по данным наблюдения за входными и выходными сигналами объекта на конечном интервале времени построить такую математическую модель, которая бы оптимально описывала изучаемый объект относительно заданного критерия (например, построение уравнений методом наименьших квадратов).

2.4. Этапы формирования модели системы

Обобщенная структурная схема формирования модели системы представлена на рис.10.

После построения модели ее следует подвергнуть проверке. Существует несколько аспектов проверки адекватности.

Во-первых, сама математическая основа модели должна быть непротиворечивой и подчиняться всем обычным законам математической логики.

Во-вторых, справедливость модели определяется ее способностью адекватно описывать исходную ситуацию.

В зависимости от сложности аналитического описания системы выделяют следующие основные способы исследования математических моделей:

§ аналитическое исследование;

§ качественное исследование;

§ исследование с помощью численных методов;

§ имитационное моделирование.

Проведение аналитического исследования предполагает наличие достаточно полного и точного аналитического описания системы в целом. Как правило, математическая модель в первоначальном виде непригодна для непосредственного исследования (например, она может не содержать в явном виде интересующие величины).

В этом случае необходимо преобразовать первоначальную модель относительно искомых величин так, чтобы было возможно получение результата аналитическими методами.

При этом появляется возможность получить достаточно полную информацию о функционировании изучаемых объектов. Однако применить такое исследование на практике удается сравнительно редко.

Качественные исследования проводят тогда, когда, не имея решения в явном виде, тем не менее, можно найти некоторые свойства решения, например, оценить устойчивость решения и т.п.

При исследовании систем с помощью численных методов после преобразования модели в систему уравнений относительно искомых величин находится решение путем реализации соответствующего численного метода.

Однако решение задачи при этом обычно бывает менее полным по сравнению с аналитическим исследованием, так как не выявляет структуры и характера функционирования системы в целом, а лишь позволяет оценить ее состояние при выбранных численных значениях параметров.

Применение численных методов стало особенно эффективным с использованием современных средств вычислительной техники. Однако применение ЭВМ не имеет здесь принципиального значения, так как ограничивается лишь автоматизацией вычислений.

2.5. Имитационное моделирование

Имитационные модели не способны формировать решение в таком виде, как в аналитических моделях, а служат лишь средством для анализа поведения системы в условиях, которые определяются экспериментатором. Поэтому имитационное моделирование является экспериментальной и прикладной методологией, имеющей целью:

§ описать поведение системы;

§ построить теории и гипотезы, которые могут объяснить наблюдаемое поведение;

§ использовать эти теории для предсказания будущего поведения системы.

Имитационное моделирование целесообразно применять при наличии любого из следующих условий:

1. Аналитические методы имеются, но очень сложны и трудоемки и имитационное моделирование дает более простой способ решения.

2. Аналитические решения имеются, но их реализация невозможна из-за недостаточной подготовки имеющегося персонала. В этом случае сопоставляются затраты на имитационное моделирование и затраты на приглашение сторонних специалистов.

3. Кроме оценки определенных параметров необходимо осуществлять наблюдение за ходом процесса в течение определенного периода.

4. Имитационное моделирование может быть единственно возможным вследствие трудности постановки эксперимента и наблюдения явлений в реальных условиях.

5. Требуется изменение масштаба времени эксперимента (как замедление, так и ускорение).

Однако имитационное моделирование имеет ряд сложностей, которые заключаются в следующем:

1. Разработка хорошей имитационной модели часто обходится дорого и требует много времени и высококвалифицированных специалистов.

2. Имитационное моделирование в принципе неточно и трудно оценить степень его точности. Частично это можно преодолеть путем анализа чувствительности модели к изменению определенных параметров.

3. Имитационное моделирование в действительности не отражает реального положения вещей и это необходимо учитывать.

4. Результат имитационного моделирования обычно является численным, а его точность определяется количеством знаков после запятой. Поэтому при имитационном моделировании числовому параметру могут приписывать большую значимость, чем есть на самом деле.

Так как имитация представляет собой крайнее средство, применяемое для решения задач, то, если задача может быть сведена к простой модели и решена аналитически, нет необходимости в имитации. Также по мере накопления информации о решаемой задаче вопрос о целесообразности применения имитации следует подвергать переоценке.

Кроме того, имитация сложных процессов требует применения мощных ЭВМ и большой выборки данных, поэтому издержки при моделировании велики по сравнению с аналитическими моделями.

Процесс имитационного моделирования можно представить в виде схемы (рис.11).