Определение. Дифференциальное уравнение первого порядка называется линейным, если оно содержит искомую функцию y и ее производную 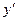 в первой степени и не содержит их произведений.
в первой степени и не содержит их произведений.
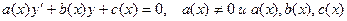 - непрерывные заданные функции. (1)
- непрерывные заданные функции. (1)
Разделим почленно на a(x), получим
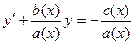 ,
, 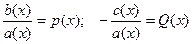 ,
,
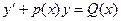 (2)
(2)
Существует несколько приемов решения линейного дифференциального уравнения. Мы изложим прием Иоганна Бернулли. Он основан на простом замечании, что любую величину y (переменную) можно представить в форме произведения двух сомножителей y=uv.
Уравнение (2) интегрируется с помощью подстановки
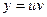 (3),
(3), 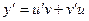 (4)
(4)
Подставив (3) и (4) в уравнение (2), получим
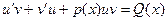
Сгруппируем члены в левой части равенства
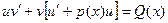
Определим функцию u так, чтобы коэффициент при v обратился в ноль.
Тогда 
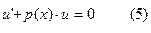
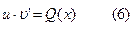
Решая (5) находим частное решение, а решая (6) – общее решение.
Методом Бернулли решение уравнения (2) сводится к решению двух уравнений с разделяющими переменными.
а) Решение (5):
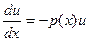 ;
; 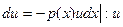 ;
; 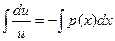 ;
; 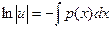 ;
; 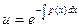 (7)
(7)
б) Решение (6): 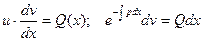
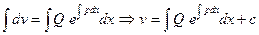 (8)
(8)
Возвращаясь к переменной y, получим
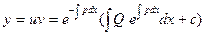 (9)
(9)
Пример: Проинтегрировать уравнение
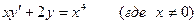
Решение. Разделим обе части уравнения на х.
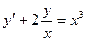 ;
; 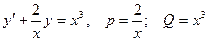 ;
;
Подстановка: 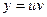 ,
, 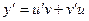 ,
,
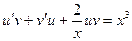 ,
, 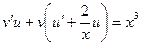
1) 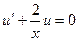 2)
2) 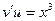
Решение (1): 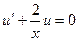 ,
, 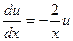 ,
, 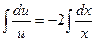 ,
, 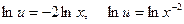 ,
, 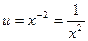
Решение (2): 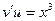 ,
, 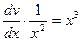 ,
,
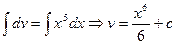
Общее решение данного уравнения имеет вид:
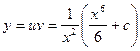
 2014-02-24
2014-02-24 396
396








