Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Определение. Линейным однородным дифференциальным уравнением II порядка с постоянными коэффициентами называется уравнение вида

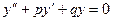(1)

где p и q – постоянные.

Если 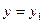- решение уравнения (1), то и 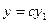, где С – произвольная постоянная, также будет решением этого уравнения.

Два решения 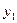и 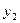уравнения (1) называются линейно зависимыми на некотором промежутке 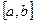, если их отношение 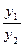равно постоянному числу с, т.е. 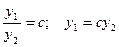. В противном случае решения (функци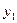и) и 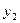линейно независимы на этом промежутке.

Есл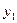и и 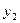- решения уравнения (1), то их сумма 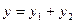также есть решение этого уравнения.

Есл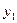и и 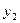- независимые решения уравнения (1); то 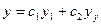(2) - общее решение этого уравнения.

Если решения уравнения (1) 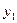и 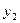линейно зависимые, то решение 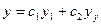не будет общим решением уравнения.

Решение 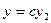является частным решением уравнения (1), т.к. оно содержит одну произвольную постоянную С.

Будем искать частные решения уравнения (1) в виде показательной функции

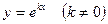(3)

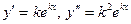. Подставив значения 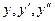в уравнение (1), получим

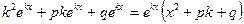(4)

Очевидно, что 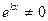, поэтому выражение (4) тождественно равно нулю тогда, когда 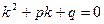(5)

Это уравнение называется характеристическим уравнением. Таким образом, 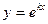- решение уравнения (1), если k является корнем характеристического уравнения.

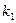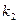1. Если характеристическое уравнение имеет два различных действительных корня и , то общее решение уравнения (1) имеет вид

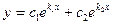(6)

2. Если характеристическое уравнение имеет два различных действительных корня , то общее решение уравнения (1) имеет вид

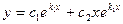, т.е. 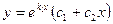(7)

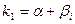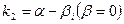3. Если корни характеристического уравнения комплексные и , то общее решение уравнения (1) выражается формулой

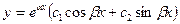(8)

Пример 1. Найти общее решение уравнения

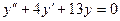
Решение. 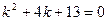, т.к.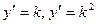

D=16-4·13<0.

D= -36 = 6² i²; 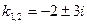- корни комплексные

,

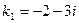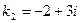
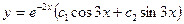-общее решение.

Пример 2.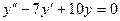

Решение.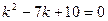

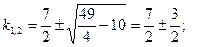
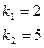
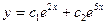- общее решение.

Итак, практическая трудность при решении линейного однородного уравнения с постоянными коэффициентами состоит единственно в решении соответствующего характеристического уравнения.