Решение линейного дифференциального уравнения методом вариации произвольной постоянной

Для решения линейного дифференциального уравнения первого порядка 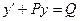(1)

можно применить и другой метод, так называемый метод вариации произвольной постоянной.

Рассмотрим соответствующее уравнение без свободного члена 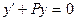(2)

В этом уравнении переменные разделяются, и его общее решение находится сразу

, ,

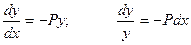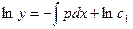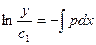. Потенцируем последнее равенство:

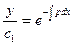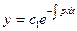, (3)

Общее решение (1) будем искать из (3), заменяя в ней произвольную постоянную 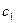некоторой дифференцируемой функцией c(x), тогда (3) выглядит так:

, =

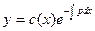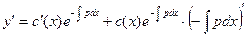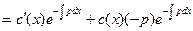
Подставляя в (1) имеем: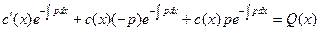

;

.

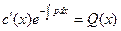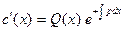
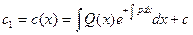Подставляя в (3), получим окончательное решение

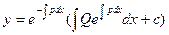
Пример. 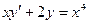(4)

Решение. , ;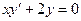

; ; ;

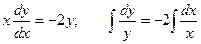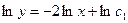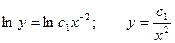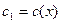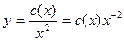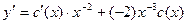; .(5)

Подставляем в данное уравнение:

;

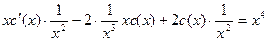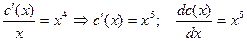
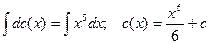(6)

Подставляя (6) в (5), имеем:

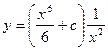- общее решение данного уравнения.