Квадратичная функция

1) y=x²

а) D(y)=R;

б) х=0, то у=0, следовательно график проходит через начало координат;

в) y>0 при x 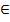R\{0};

г) y(-x)=y(x), следовательно функция четная, график симметричен относительно оси Оу;

д) при х 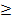0 возрастает, при х 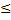0 убывает

е) х=0 – точка минимума.

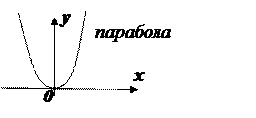
2 ) y=аx²

3)

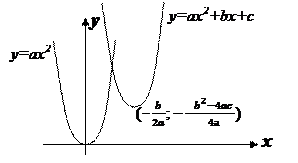y= a (x² + 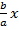)+c = a (x² + 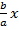+ 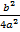) – 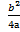+c= a (x + 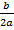)² – –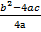

Итак, график функции y=ax²+bx+c парабола, полученная из графика функции y=ax²

Вывод: 1) Если d<0, то при а>0 график функции весь лежит выше оси абсцисс, и при а<0 ниже оси абсцисс.

2) Если d=0, вершина параболы лежит на оси Ох, если а>0 в верхней полуплоскости, если а<0 в нижней полуплоскости.

3) Если d>0, то график функции пересекает ось Ох в двух точках, при а>0 «ветви» вверх, при а<0 «ветви» вниз.