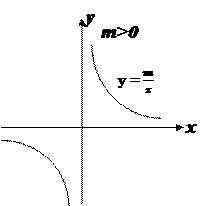1) у=хn, n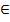 N
N
|
(биссектриса I и III координатных углов)
n=2, у=х2 – парабола
 а) D(y)=R
а) D(y)=R
б) у=0, то х=0, значит график проходит через начало координат.
в) n=2k (четное) у(-х)=у(х), следовательно, функция четная
n=2k+1 (нечетное) у(-х)= –у(х), следовательно, функция нечетная
г) n=2k 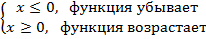
n=2k+1, x 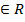 функция возрастает
функция возрастает
При n=3 график называется кубической параболой.
2) у=xn, n=-1
2.1 у =  , общий случай у =
, общий случай у =  – обратная пропорциональность, m – коэффициент обратной пропорциональности.
– обратная пропорциональность, m – коэффициент обратной пропорциональности.
Свойства функции у = 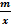 :
:
1) D(y)=R\{0};
2) E(y)=R\{0}, нулей функции нет;
3) у(-х)=-у(х) – функция нечетная, график симметричен относительно начала координат;
4) m>0. Если x>0, y>0, еcли x<0, y<0;
5) x>0, x1<x2, то 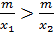 , у1>у2, функция убывает
x<0, x1<x2, то , у1>у2, функция убывает
x<0, x1<x2, то 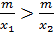 , у1>у2, функции убывает , у1>у2, функции убывает
Функция убывает на всей области определения. 6) у = х→ –
| m<0. Если x>0, y<0, еcли x<0, y>0 Самостоятельная работа № 3 Свойства разобрать |
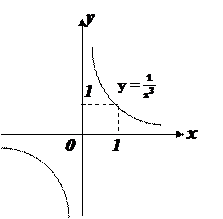
График: равнобочная гипербола.
2.2 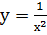
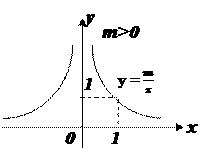
2.3 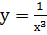
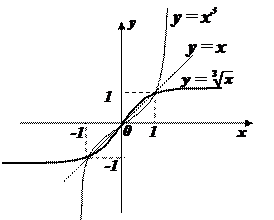 § 10 Степенная функция с дробным показателем.
§ 10 Степенная функция с дробным показателем.
1. Рассмотрим функцию 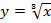 , являющуюся обратной к функции у=х3, следовательно ее график симметричен кубической параболе у=х3 относительно биссектрисы I и III координатных углов.
, являющуюся обратной к функции у=х3, следовательно ее график симметричен кубической параболе у=х3 относительно биссектрисы I и III координатных углов.
Свойства:
1) D(y)=R;
2) E(y)=R;
3) у(-х)=-у(х) – функция нечетная;
4) (0;0) – нуль функции;
5) возрастает на всей области определения
6) максимумов, минимумов нет;
7) асимптот нет.
2. 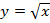 на промежутке [0; +
на промежутке [0; +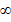 ). На данном промежутке функция у=х2 монотонна, а следовательно имеет обратную.
). На данном промежутке функция у=х2 монотонна, а следовательно имеет обратную.
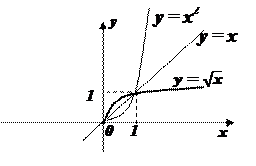
3. 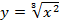 график называется полукубической параболой
график называется полукубической параболой
1) D(y)=R;
2) 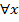 , у
, у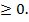 у=0 при х=0, следовательно, график проходит через начало координат и лежи т в верхней полуплоскости;
у=0 при х=0, следовательно, график проходит через начало координат и лежи т в верхней полуплоскости;
3) у(-х)=у(х) – функция четная, график симметричен относительно оси ординат;
4)
|
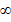 ; 0) – убывает; (0; +
; 0) – убывает; (0; +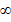 ) – возрастает.
) – возрастает.
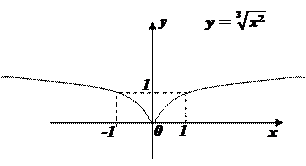
 2014-02-24
2014-02-24 1530
1530

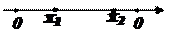
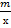 х→ +
х→ +