Комплексные числа. Топология расширенной комплексной плоскости

ГЛАВА 10 ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Опр Мнимой единицей называется символ 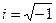. Комплексным числом (в алгебраической форме) называется выражение вида .

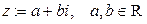ЗАМЕЧ Эйлер обозначал мнимую единицу 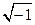. Обозначение 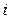предложил Гаусс. Понятие комплексного числа появилось у Кардано (1545), а термин ввел Карно (1803). Теория комплексных чисел развита Гауссом (1831).

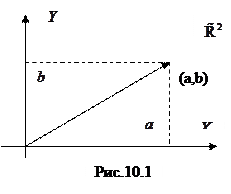
Опр (Вессель, 1799, Арган, 1806) Каждой точке с радиусом-вектором 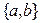евклидовой плоскости 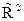(Рис.10.1) с ПДСК сопоставим комплексное число 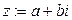. Тем самым устанавливаем взаимно однозначное соответствие между векторами 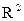и множеством комплексных чисел . Ось абсцисс назовем вещественной осью и обозначим 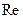. Ось ординат - мнимой осью и обозначим 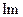. Единицей измерения на последней будет 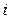. Совокупность точек и так переименованных осей называется комплексной плоскостью (Рис.10.2), которую будем обозначать той же буквой .

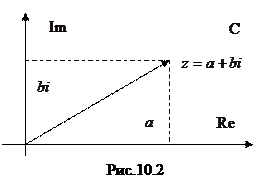
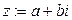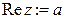Опр Для число называется вещественной частью, а число 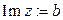- коэффициентом мнимой части комплексного числа .

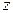Опр Суммой (разностью) комплексных чисел 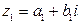, 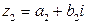называется комплексное число .

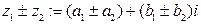Опр (Бомбелли, 1572) Произведением комплексных чисел 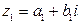, 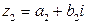называется комплексное число .

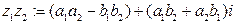Опр (Коши, 1831) Комплексное число 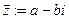называется сопряженнымк комплексному числу 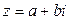. Пример .

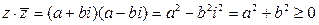Опр (Арган, 1814) Модулем комплексного числа 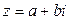называется число .

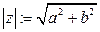ЗАМЕЧ 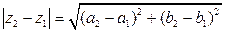, то есть модуль разности комплексных чисел совпа дает с расстоянием между соответствующими точками 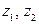комплексной плоскости .

Опр Частным от деления комплексных чисел 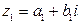, 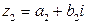называется комплексное число .

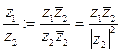Опр (Коши,1847) Главным значением аргумента комплексного числа 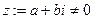называется величина угла 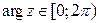между положительным направлением вещественной оси и направлением на точку 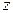, отсчитываемого против часовой стрелки.(лат. argumentum – знак).

ЗАМЕЧ Функция 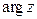, определена на 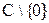, и определяет бесконечнозначную функцию .

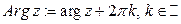Опр Если 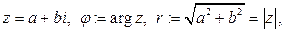то выражение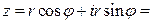

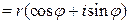называется тригонометрической формой комплексного числа.

Обозначение 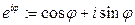- формула Эйлера (1740).

Опр 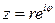- показательная форма комплексного числа.

ТЕОРЕМА 10.1 Пусть 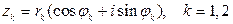. Тогда:

1) 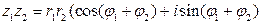; 2) ;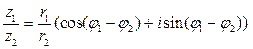

3) алгебраическое уравнение 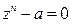имеет ровно 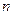комплексных корней, которые вычис ляются по формул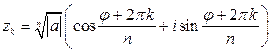е , где .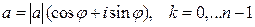

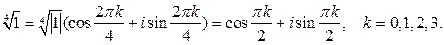
Опр Для комплексного числа .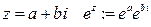

СЛЕДСТВИЕ Для комплексных чисел .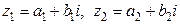

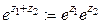ЗАМЕЧАНИЕ (электротехнический смысл комплексного числа) Если переменные напряжение или ток в цепи изменяются по гармоническому закону: 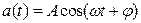, где 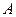- амплитуда колебаний, 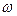- угловая частота, 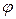- начальная фаза, то комплексной амплитудой колебаний называется комплексное число .

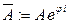Пример Комплексная амплитуда линейной комбинации 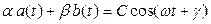гармонических колебани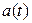й и 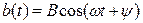с одинаковой частотой 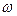равна линейной комбинации комплексных амплитуд: .

_____

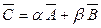Опр Добавим к комплексной плоскости одну “бесконечно удаленную точку” 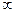. Полученное множество называется расширеннойкомплексной плоскостью (сферой Римана) и обозначается 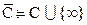. 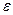- окрестностью конечной точки называется круг 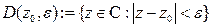. 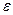- окрестностью бесконечно удаленной точки 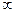называется множество 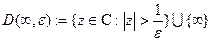. При таком определении очевидно 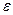-окрестность стягивается к своему центру, когда .

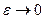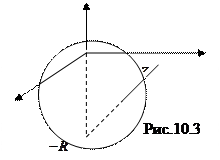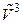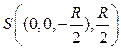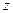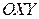ЗАМЕЧАНИЕ Построим в с ПДСК сферу . Сопоставим каждой точке комплексной плоскости , отождествляемой с , точку пересечения сферы с отрезком, соединяющим «южный полюс» 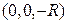и 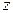(Рис.10.3). Точке 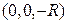сопоставим 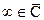. Это соответствие называется стереографической проекцией, и устанавливает гомеоморфизм между точками нашей сферы и сферой Римана 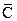, что и объясняет название последней. Когда переменная точка 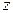на сфере приближается к “южному полюсу”, соответствующая ей стереографическая проекция на плоскости приближается к точке 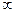. Тем самым 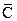удобно представлять в виде сферы сколь угодно большого радиуса, северный полюс которой совпадает с началом координат, а южный – с бесконечно удаленной точкой.

_____

Опр Пусть комплекснозначная функция (КЗФ) 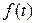определена в окрестности точки 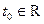и принимает значения в 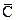. Говорят, что 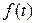имеет предел 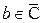при 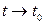, если

.

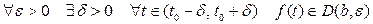Пр (электротехнический смысл КЗФ) Комплексные сопротивления емкости 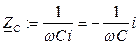, комплексные сопротивления индуктивности 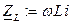и входное сопротивление двухполюсника являются комплекснозначными функциями от частоты .

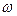Опр Комлекснозначная функция (КЗФ) 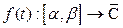называется непрерывной в точке 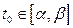, если .

____

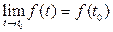ЗАМЕЧАНИЕ Пусть дана непрерывная КЗФ 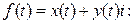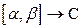. Как и в случае евклидовой плоскости определяются кривые 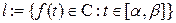замкнутая, спрямляя емая и гладкая кривые. В последнем случае условие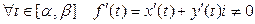

равносильно существованию касательной в каждой точке этой кривой.

Опр Кривая называется жордановой, если КЗФ 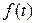взаимнооднозначна, то есть кривая не имеет точек самопересечения. Кривая называется замкнутой жордановой, если она замкнута и сужение 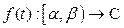взаимнооднозначно.

Пр Окружность 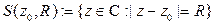, задаваемая КЗФ 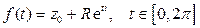, есть гладкая жорданова замкнутая кривая.

Опр Совокупность 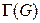граничных точек множества 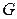называется границеймножества. Множество 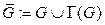называется замыканием множества 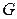. Множества 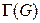и 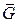всегда замкнуты.

Пр .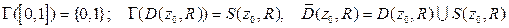

Опр Множество 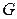называется несвязным, если его можно разбить на два подмножества, каждое из которых не содержит предельных точек другого подмножества. В противном случае множество называется связным.

Пр 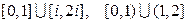- несвязные множества. 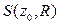- связное множество.