Вывод уравнений Лагранжа 2-го рода

Рассмотрим движение системы из N мат. точек относительно инерциальной системы отсчета. Если некоторые связи не идеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам.

Общее уравнение динамики для такой системы имеет вид

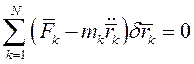(1)

Пусть система имеет n степеней свободы и её положение определяется 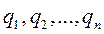обобщенными координатами 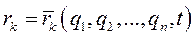. Возможное перемещение k -й точки

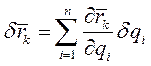(2)

Подставляя (2) в (1) и изменяя порядок суммирования получаем

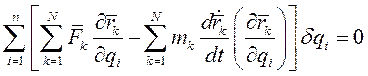(3)

В этом выражении 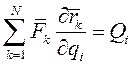- обобщенная сила, соответствующая i -й координате. Преобразуем выражение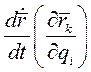

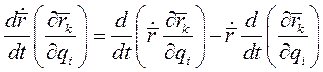(4)

Так как 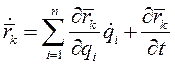, то

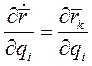(5)

Равенство (4) называется первым тождеством Лагранжа.

Заменив на основании этого тождества производную 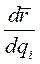на 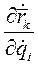в первом слагаемом выражения (5), получим

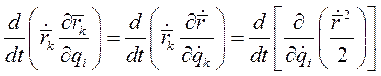
Следовательно

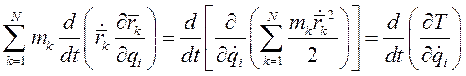(I)

Где Т – кинетическая энергия механической системы

Преобразуем теперь производную 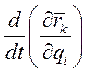. Так как 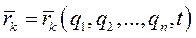, то 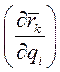- функция обобщенных координат и времени. Поэтому, с одной стороны,

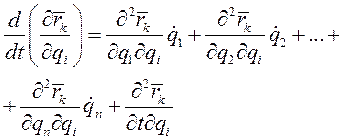(6)

С другой стороны

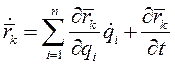
и

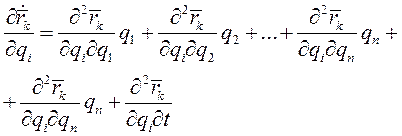(7)

Сопоставляя (5) и (6) заключаем, что

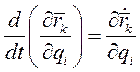(8)

Это второе тождество Лагранжа.

М учетом данного тождества получаем

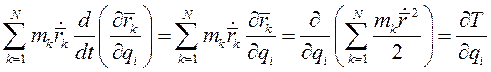(II)

Подставляя в общее уравнение (3) выражение для обобщенной силы 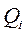б а также результаты преобразований (I) и (II), находим

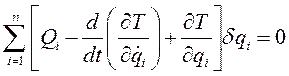(III)

Вариации обобщенных координат независимы между собой, поэтому условие (III) будет выполнено, если равны нулям множители при всех 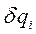, т.е. если

(*)

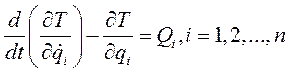Уравнения (*) называются уравнениями Лагранжа второго рода.

35. Момент инерции твёрдого тела относительно оси, проходящей через заданную точку в заданном направлении.

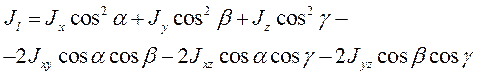
Моменты инерции относительно осей координат

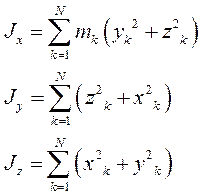
Центробежные моменты инерции относительно тех же осей.

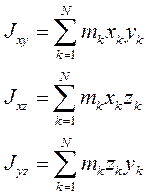
Тензор инерции:

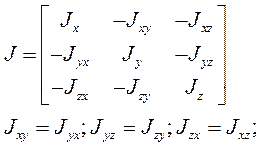
36. Эллипсоид инерции. Главные оси инерции симметричных твёрдых тел.

Эллипсоид инерции – поверхность второго порядка, построенная в любой точке тела – характеризует спектр моментов инерции тела относительно осей, проходящих через эту точку.

Для построения этой поверхности на каждой из оси Ol, проходящей через точку О, откладывают от этой точки отрезок

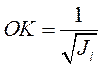
Главные оси (симметрии) эллипсоида инерции, построенного в точке твёрдого тела, называют главными осями инерции для данной точки тела.

Если оси координат направить по взаимно перпендикулярным главным осям эллипсоида инерции (OX, OY, OZ), то его уравнение будет иметь вид

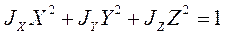(1)

Эллипсоид инерции, построенный для центра масс тела, называется центральным эллипсоидом инерции, а его главные оси – главными центральными осями инерции тела. В формуле это 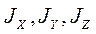. Моменты инерции относительно главных центральных осей инерции называют главными центральными моментами инерции тела и обозначают

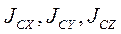. Сравнив (1) с уравнением эллипсоида в канонической форме

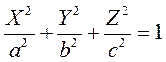
получим

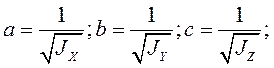
Эллипсоид называется трёхосным, если все главные моменты инерции для точки тела различны, и эллипсоидом вращения, если два главных момента инерции для точки тела равны.

37. Кинетический момент твёрдого тела, вращающегося вокруг неподвижной точки.

38. Кинетическая энергия твёрдого тела при движении вокруг неподвижной точки.

39. Вывод кинематических и динамических уравнений Эйлера.

40. Приближённая теория гироскопа. Основные понятия и допущения.

41. Особенности движения оси гироскопа. Теорема Резаля. Правило прецессии.

42. Гироскопический момент. Правило Жуковского.