Для равновесия системы, подчиненной голономным удерживающим связям, необходимо и достаточно, чтобы обобщенные силы, соответствующие всем обобщенным координатам системы, были равны нулю.
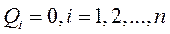
|
Положим, что механическая система из N точек, в силу наложенных на неё голономных удерживающих связей имеет n степеней свободы. Положение такой системы в пространстве определяется обобщенными координатами 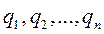 , и радиус-вектор k -й точки есть функция обобщенных координат:
, и радиус-вектор k -й точки есть функция обобщенных координат:
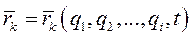
Возможное перемещение каждой точки системы
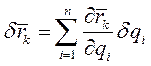
Подставляя выражение для 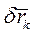 в условие равновесия системы
в условие равновесия системы 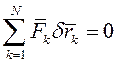 получаем
получаем
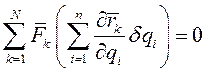
После изменения порядка суммирования это условие принимает вид
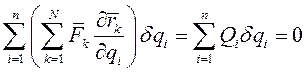 (I)
(I)
Так как обобщенные координаты независимы, то их вариации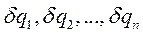 тоже будут независимы между собой. Поэтому условие (I) будет выполнено, если равны нулю обобщенные силы, соответствующие всем обобщенным координатам системы
тоже будут независимы между собой. Поэтому условие (I) будет выполнено, если равны нулю обобщенные силы, соответствующие всем обобщенным координатам системы
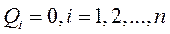
Если силы, приложенные к точкам механической системы, потенциальные, то
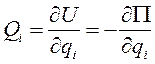
В этом случае условия равновесия имеют вид
|
|
|
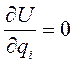 или
или 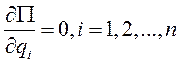
 2014-02-24
2014-02-24 3383
3383
