Проверка гипотезы о показательном распределении генеральной совокупности

Лекция №9

Тема 13: «Математическая статистика».

Время: 2 часа

Цель лекции: Ознакомить слушателей с методами статистической проверки статистических гипотез;

Учебные вопросы:

· Проверка гипотезы о показательном распределении генеральной совокупности;

· Проверка гипотезы о распределении генеральной совокупности по биномиальному закону;

· Проверка гипотезы о равномерном распределении генеральной совокупности;

· Проверка гипотезы о распределении генеральной совокупности по закону Пуассона;

· Проверка гипотезы о нормальном распределении генеральной совокупности;

Задано эмпирическое распределение непрерывной случайной величины Х в виде последовательности интервалов 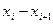и соответствующих им частот 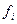(или 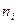), причем 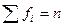(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина Х имеет показательное распределение.

Правило. Для того, чтобы при уровне значимости 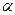проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:

1. Найти по заданному эмпирическому распределению выборочную среднюю 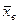. Для этого, приняв в качестве "представителя" i-го интервала его середину 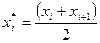, составляют последовательность равноотстоящих вариант и соответствующих им частот.

2. Принять в качестве оценки параметра 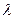показательного распределения величuну, обратную выборочной средней:

.

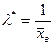3. Найти вероятности попадания Х в частичные интервалы 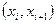по формуле

.

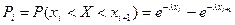4. Вычислить теоретические частоты:

,

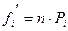где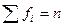 объем выборки.

5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы 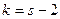, где s - число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s - число интервалов, оставшихся после объединения.